Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 10 tập 2 theo chương trình Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải Hoạt động 2 trang 89 một cách dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
Đề bài
Thực hành 2 trang 89 SGK Toán 10 tập 2 – CTST
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) \(\)\(y = {x^2} - 3x + 2\)
b) \(y = {x^2}\)
c) \(y = - {x^2}\)
d) \(y = 2{x^2} + 1\)
e) \(y = - \frac{1}{2}{x^2} + 4\)
Phương pháp giải - Xem chi tiết
Bước 1:Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
Bước 2: Tạo các thanh trượt biểu thị các tham số a, b, c bằng cách nhấp chuật liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt (hình 4)
+) Nhập công thúc hàm số bậc hai \(y = a{x^2} + bx + c\) tại vùng nhập lệnh theo cú pháp: y = ax^2 + bx + c
+) Nhập công thức \(\Delta = {b^2} - 4ac\) bằng cách gõ: D = b^2 - 4ac
+) Quan sát đồ thị được vẽ trên vùng làm việc
+) Dùng chuột điều chỉnh các thanh trượt a, b, c để có giá trị mong muốn
+) Quan sát sự thay đổi của hình dạng đồ thị (parabol) và \(\Delta \) theo sự thay đổi các hệ số a, b, c trong công thức hàm số
Bước 3: Nêu kết luận về tính chất của đồ thị quan sát được trên hình vẽ
Lời giải chi tiết
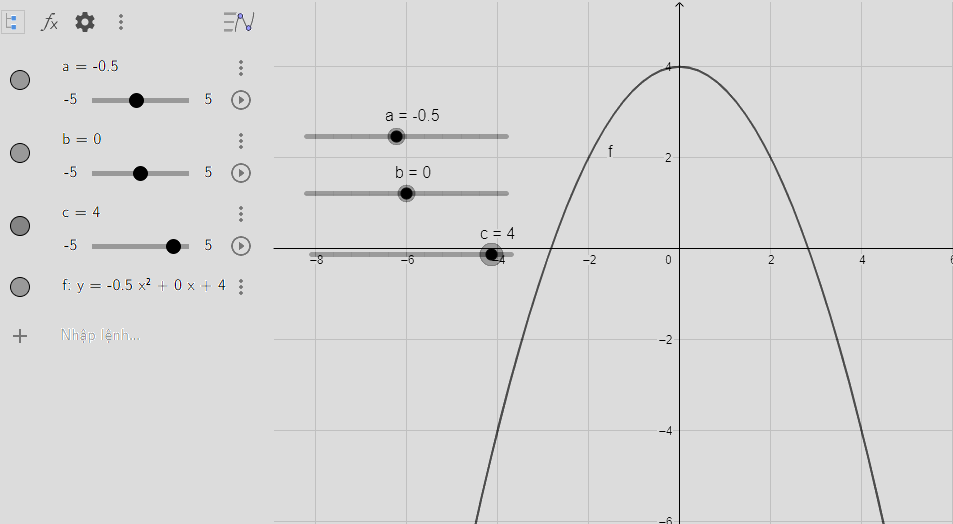
Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây
a) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0)
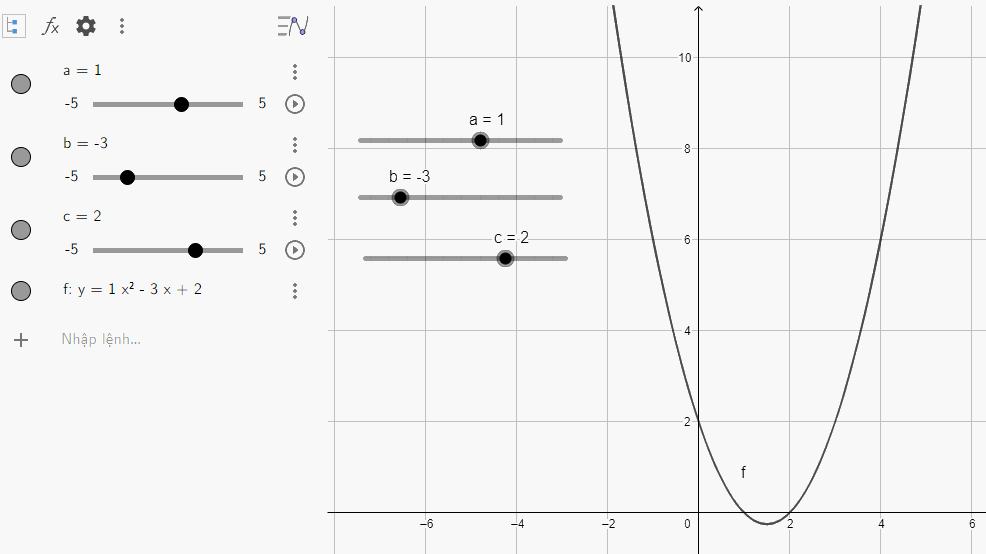
b) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
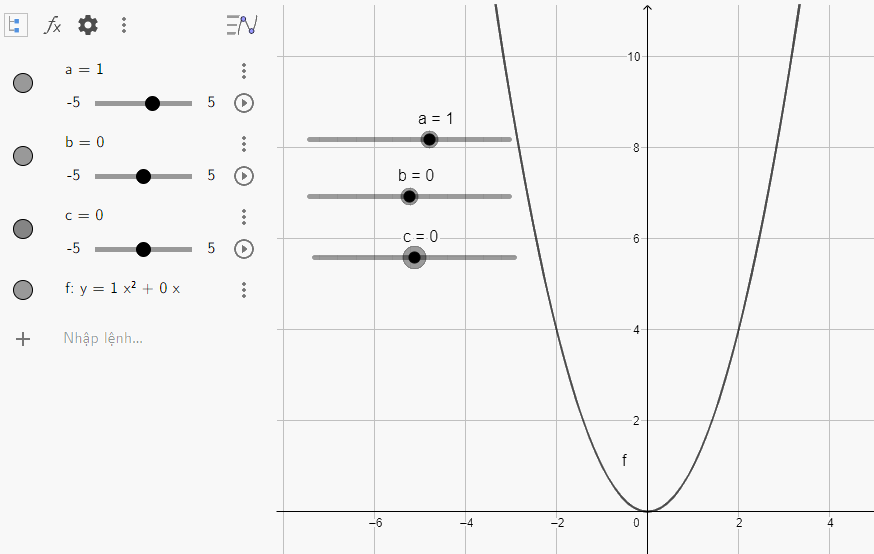
c) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
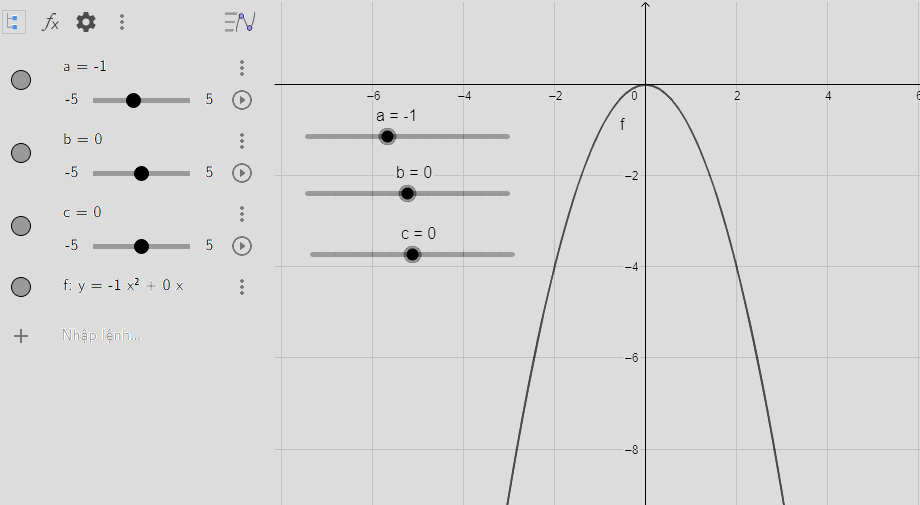
d) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
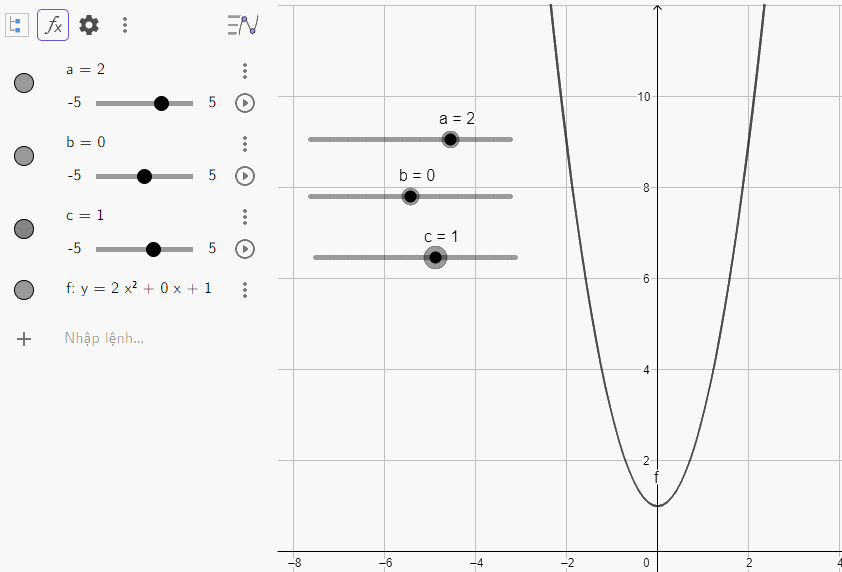
e) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol
Hoạt động 2 trang 89 SGK Toán 10 tập 2 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết một bài toán thực tế. Bài toán này thường liên quan đến việc xác định vị trí của một điểm trong không gian dựa trên các vectơ chỉ hướng và vectơ gốc.
Trước khi đi vào giải bài toán, chúng ta cần phân tích kỹ đề bài để xác định rõ các yếu tố sau:
Sau khi xác định rõ các yếu tố này, chúng ta có thể sử dụng các phép toán vectơ để tìm ra tọa độ của điểm đích.
Để giải Hoạt động 2 trang 89, chúng ta có thể sử dụng phương pháp sau:
Giả sử chúng ta có một bài toán như sau:
Một người đi bộ từ điểm A(1; 2) theo hướng vectơ u = (3; 1) một đoạn đường bằng độ dài của vectơ u. Hỏi người đó đến điểm nào?
Giải:
Khi giải các bài toán liên quan đến vectơ, cần chú ý đến các quy tắc sau:
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Hoạt động 2 trang 89 SGK Toán 10 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và các phép toán vectơ. Bằng cách phân tích bài toán, áp dụng phương pháp giải phù hợp và thực hành các bài tập vận dụng, bạn sẽ nắm vững kiến thức và tự tin giải các bài toán tương tự.
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải quyết bài toán Hoạt động 2 trang 89 một cách hiệu quả. Chúc bạn học tập tốt!