Chào mừng bạn đến với bài học lý thuyết về Ba đường conic trong mặt phẳng tọa độ, thuộc chương trình SGK Toán 10 Chân trời sáng tạo. Đây là một chủ đề quan trọng, đặt nền móng cho các kiến thức hình học giải tích nâng cao hơn.
Chúng tôi tại giaitoan.edu.vn sẽ cung cấp cho bạn một cách tiếp cận toàn diện, từ định nghĩa, phương trình đến các tính chất đặc trưng của Elip, Hypebol và Parabol.
A. Lý thuyết 1. Elip a) Nhận biết elip
A. Lý thuyết
1. Elip
a) Nhận biết elip
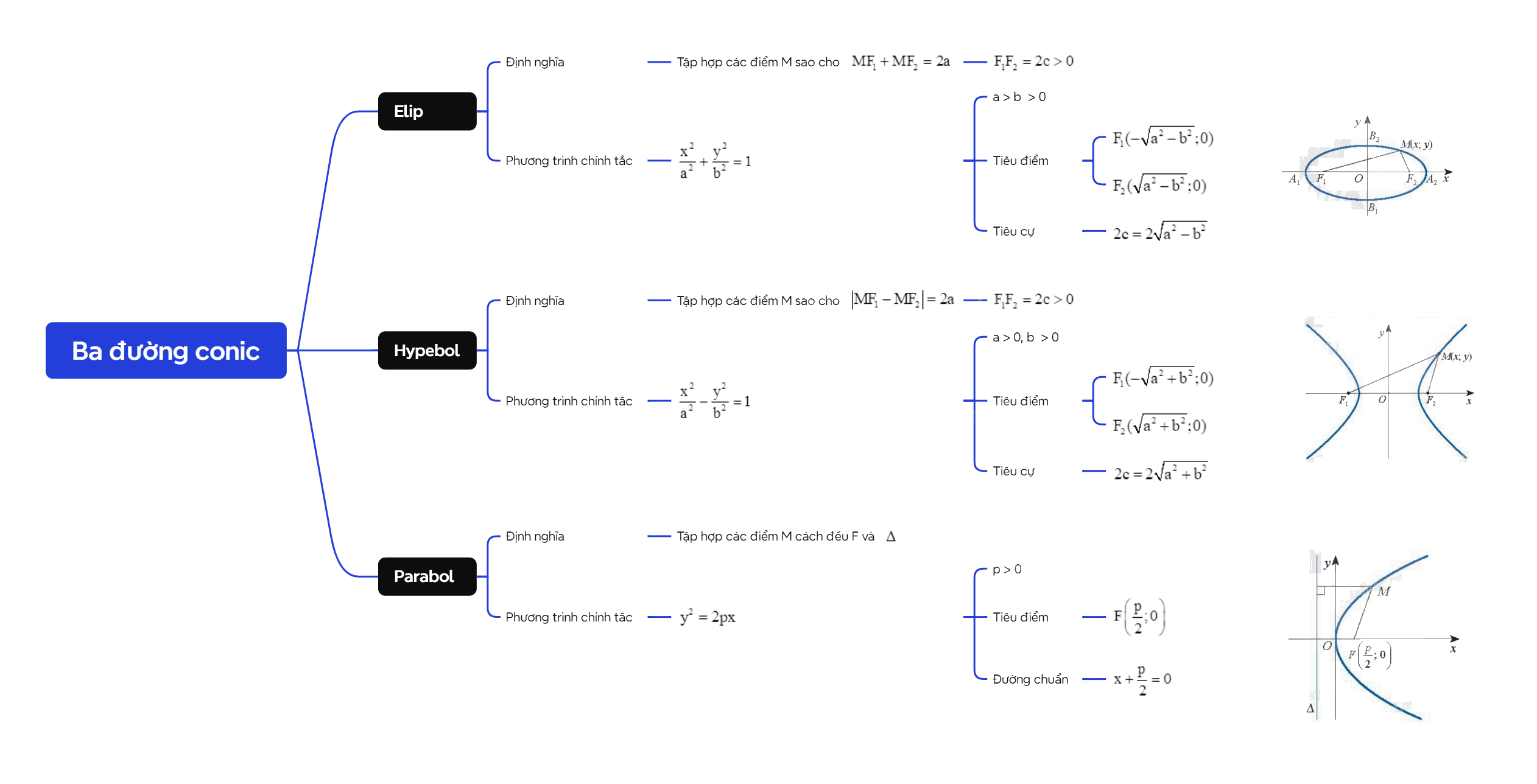
| Cho hai điểm \({F_1}\), \({F_2}\) cố định có khoảng cách \({F_1}{F_2} = 2c > 0\). Cho số thực a > c. Tập hợp các điểm M sao cho \(M{F_1} + M{F_2} = 2a\) được gọi là đường elip (hay elip). Hai điểm \({F_1}\), \({F_2}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của elip đó. |
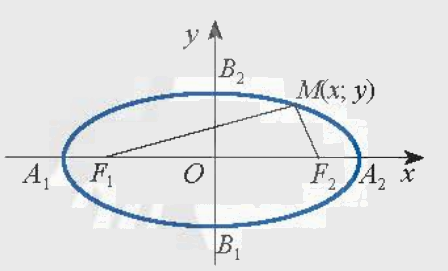
b) Phương trình chính tắc của elip
Trong mặt phẳng tọa độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó thì có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với a > b > 0. Ngược lại, mỗi phương trình có dạng trên đều là phương trình của elip có hai tiêu điểm \({F_1}( - \sqrt {{a^2} - {b^2}} ;0)\), \({F_2}(\sqrt {{a^2} - {b^2}} ;0)\), tiêu cự \(2c = 2\sqrt {{a^2} - {b^2}} \) và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a. |
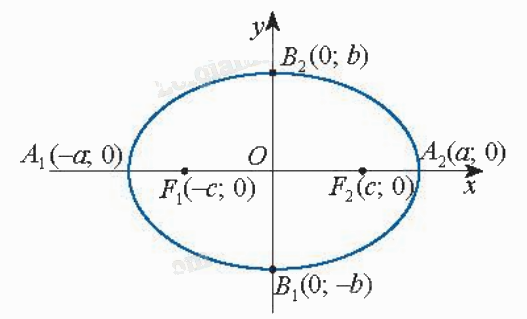
Chú ý:
- Elip (E) cắt Ox tại hai điểm \({A_1}( - a;0)\), \({A_2}(a;0)\) và cắt Oy tại hai điểm \({B_1}(0; - b)\), \({B_2}(0;b)\).
- Các điểm \({A_1}\), \({A_2}\), \({B_1}\), \({B_2}\) gọi là các đỉnh của elip.
- Đoạn thẳng \({A_1}{A_2}\) gọi là trục lớn, đoạn thẳng \({B_1}{B_2}\) gọi là trục nhỏ của elip.
- Giao điểm O của hai trục gọi là tâm đối xứng của elip.
- Nếu \(M(x;y) \in (E)\) thì \(\left| x \right| \le a\), \(\left| y \right| \le b\).
2. Hypebol
a) Nhận biết hypebol
| Cho hai điểm \({F_1}\), \({F_2}\) cố định có khoảng cách \({F_1}{F_2} = 2c > 0\). Cho số thực dương a < c. Tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2a\) được gọi là đường hypebol (hay hypebol). Hai điểm \({F_1}\), \({F_2}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của hypebol đó. |
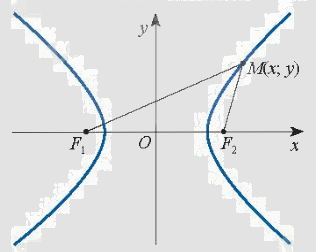
b) Phương trình chính tắc của hypebol
Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó thì có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a > 0, b > 0. Ngược lại, mỗi phương trình có dạng trên đều là phương trình của hypebol có hai tiêu điểm \({F_1}( - \sqrt {{a^2} + {b^2}} ;0)\), \({F_2}(\sqrt {{a^2} + {b^2}} ;0)\), tiêu cự \(2c = 2\sqrt {{a^2} + {b^2}} \) và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng 2a. |
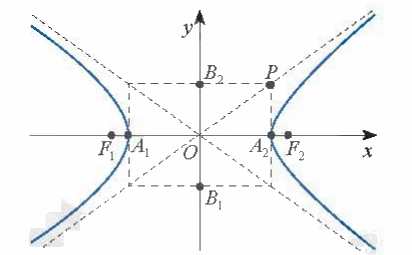
Chú ý:
- Hypebol (H) cắt Ox tại hai điểm \({A_1}( - a;0)\), \({A_2}(a;0)\). Nếu vẽ hai điểm \({B_1}(0; - b)\), \({B_2}(0;b)\) vào hình chữ nhật \(O{A_2}P{B_2}\) thì \(OP = \sqrt {{a^2} + {b^2}} = c\).
- Các điểm \({A_1}\), \({A_2}\) gọi là các đỉnh của hypebol.
- Đoạn thẳng \({A_1}{A_2}\) gọi là trục thực, đoạn thẳng \({B_1}{B_2}\) gọi là trục ảo của hypebol.
- Giao điểm O của hai trục là tâm đối xứng của hypebol.
- Nếu \(M(x;y) \in (H)\) thì \(x \le - a\), \(x \ge a\).
3. Parabol
a) Nhận biết parabol
| Cho một điểm F cố định và một đường thẳng \(\Delta \) cố định không đi qua F. Tập hợp các điểm M cách đều F và \(\Delta \) được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, \(\Delta \) được gọi là đường chuẩn, khoảng cách từ F đến \(\Delta \) được gọi là tham số tiêu của parabol đó. |
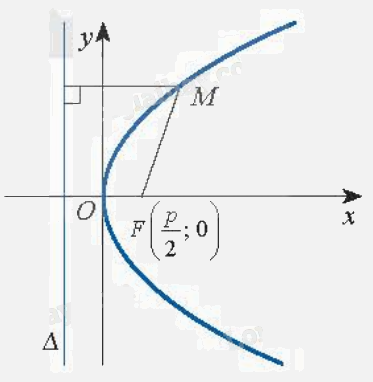
b) Phương trình chính tắc của parabol
Xét (P) là một parabol với tiêu điểm F, đường chuẩn \(\Delta \). Gọi H là hình chiếu vuông góc của F trên \(\Delta \). Khi đó, trong hệ trục tọa độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình chính tắc \({y^2} = 2px\) (với p > 0). Ngược lại, mỗi phương trình trên là phương trình chính tắc của parabol có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\) và đường chuẩn \(x + \frac{p}{2} = 0\). |
Chú ý:
- O gọi là đỉnh của parabol (P).
- Ox gọi là trục đối xứng của (P).
- p gọi là tham số tiêu của (P).
- Nếu \(M(x;y) \in (P)\) thì \(x \ge 0\) và \(M'(x; - y) \in (P)\)..
B. Bài tập
Bài 1: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip?
a) \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
b) \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = - 1\)
c) \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{4^2}}} = 1\)
d) \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
Giải:
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với a > b > 0 nên chỉ có trường hợp d) là phương trình chính tắc của elip.
Bài 2: Trong các phương trình sau, phương trình nào là phương trình chính tắc của hypebol?
a) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{4^2}}} = - 1\)
b) \(\frac{{{x^2}}}{{{4^2}}} - \frac{{{y^2}}}{{{5^2}}} = 1\)
c) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{5^2}}} = 1\)
d) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{4^2}}} = 1\)
Giải:
Phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a > 0, b > 0 nên các trường hợp b), c), d) là phương trình chính tắc của hypebol.
Bài 3: Trong các phương trình sau, phương trình nào là phương trình chính tắc của parabol?
a) \({y^2} = - 6x\)
b) \({y^2} = 6x\)
c) \({y^2} = - 6y\)
d) \({y^2} = 6y\)
Giải:
Phương trình chính tắc của parabol có dạng \({y^2} = 2px\), với p > 0 nên chỉ có trường hợp d) là phương trình chính tắc của parabol.
Bài 4: Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của elip. Tính tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
Giải:
Ta có: \({a^2} = 25\), \({b^2} = 16\). Do đó \(c = \sqrt {{a^2} - {b^2}} = 3\). Vậy elip có hai tiêu điểm là \({F_1}( - 3;0)\), \({F_2}(3;0)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\). Ta có \(a = \sqrt {25} = 5\) nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a = 10.
Bài 5: Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
Giải:
Ta có: \({a^2} = 9\), \({b^2} = 16\). Do đó \(c = \sqrt {{a^2} + {b^2}} = 5\). Vậy hypebol có hai tiêu điểm là \({F_1}( - 5;0)\), \({F_2}(5;0)\) và tiêu cự là \(2c = 10\). Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng \(2a = 2\sqrt 9 = 6\).
Bài 6: Cho parabol (P): \({y^2} = x\).
a) Tìm tiêu điểm F, đường chuẩn \(\Delta \) của (P).
b) Tìm những điểm trên (P) có khoảng cách tới F bằng 3.
Giải:
a) Ta có \(2p = 1\) nên \(p = \frac{1}{2}\).
Parabol có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\) và đường chuẩn \(\Delta :x = - \frac{1}{4}\).
b) Điểm \(M({x_0};{y_0})\) thuộc (P) có khoảng cách tới F bằng 3 khi và chỉ khi \({y_0}^2 = {x_0}\) và MF = 3. Do \(MF = d(M,\Delta )\) nên \(d(M,\Delta ) = 3\).
Mặt khác \(\Delta :x = - \frac{1}{4}\) và \({x_0} = {y_0}^2 \ge 0\) nên \(3 = d(M,\Delta ) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}\).
Vậy \({x_0} = \frac{{11}}{4}\) và \({y_0} = \frac{{\sqrt {11} }}{2}\) hoặc \({y_0} = - \frac{{\sqrt {11} }}{2}\).
Vậy có hai điểm M thỏa mãn bài toán với tọa độ là \(\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right)\) và \(\left( {\frac{{11}}{4}; - \frac{{\sqrt {11} }}{2}} \right)\).
Bài 7: Lập phương trình chính tắc của elip (E) có một tiêu điểm là \({F_2}(5;0)\) và đi qua điểm M(0;3).
Giải:
Elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0).
Do \({F_2}(5;0)\) là một tiêu điểm của (E) nên c = 5.
Điểm M(0;3) nằm trên (E) nên \(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1\). Do đó \({b^2} = 9\).
Suy ra \({a^2} = {b^2} + {c^2} = 9 + 25 = 34\).
Vậy elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{34}} + \frac{{{y^2}}}{9} = 1\).
Bài 8: Lập phương trình chính tắc của hypebol (H) có một tiêu điểm là \({F_2}(6;0)\) và đi qua điểm A(4;0).
Giải:
Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0).
Do \({F_2}(6;0)\) là một tiêu điểm của (H) nên c = 6.
Điểm A(4;0) nằm trên (H) nên \(\frac{{{4^2}}}{{{a^2}}} - \frac{{{0^2}}}{{{b^2}}} = 1\). Do đó \({a^2} = 16\).
Suy ra \({b^2} = {c^2} - {a^2} = {6^2} - 16 = 20\).
Vậy hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\).
Bài 9: Lập phương trình chính tắc của parabol (P), biết:
a) (P) có tiêu điểm là F(5;0).
b) (P) đi qua điểm M(2;1).
Giải:
Parabol (P) có phương trình chính tắc là \({y^2} = 2px\) (p > 0).
a) Do F(5;0) là tiêu điểm của (P) nên \(\frac{p}{2} = 5\), tức là p = 10.
Vậy parabol (P) có phương trình chính tắc là \({y^2} = 20x\).
b) M(2;1) nằm trên (P) nên \({1^2} = 2p.2\), tức \(p = \frac{1}{4}\).
Vậy parabol (P) có phương trình chính tắc là \({y^2} = \frac{x}{2}\).
Ba đường conic, bao gồm elip, hypebol và parabol, là những đường cong quan trọng trong hình học giải tích. Chúng xuất hiện trong nhiều lĩnh vực khoa học và kỹ thuật, từ vật lý thiên văn đến kiến trúc.
Elip là tập hợp các điểm M sao cho tổng khoảng cách từ M đến hai điểm cố định F1 và F2 (tiêu điểm) là một hằng số (2a, với a > 0).
Phương trình chính tắc của elip: x2/a2 + y2/b2 = 1 (với a > b > 0)
Hypebol là tập hợp các điểm M sao cho hiệu khoảng cách từ M đến hai điểm cố định F1 và F2 (tiêu điểm) là một hằng số (2a, với a > 0).
Phương trình chính tắc của hypebol: x2/a2 - y2/b2 = 1
Parabol là tập hợp các điểm M cách đều một điểm cố định F (tiêu điểm) và một đường thẳng cố định Δ (đường chuẩn).
Phương trình chính tắc của parabol: y2 = 2px
Ví dụ 1: Xác định các yếu tố của elip có phương trình x2/9 + y2/4 = 1
Giải: a2 = 9, b2 = 4 => a = 3, b = 2. c2 = a2 - b2 = 9 - 4 = 5 => c = √5. Tiêu điểm: F1(-√5, 0), F2(√5, 0). Tâm sai: e = √5/3.
Ví dụ 2: Xác định các yếu tố của hypebol có phương trình x2/16 - y2/9 = 1
Giải: a2 = 16, b2 = 9 => a = 4, b = 3. c2 = a2 + b2 = 16 + 9 = 25 => c = 5. Tiêu điểm: F1(-5, 0), F2(5, 0). Tâm sai: e = 5/4. Tiệm cận: y = ±(3/4)x.
Ba đường conic có nhiều ứng dụng trong thực tế:
Để nắm vững kiến thức về ba đường conic, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm các bài tập trong SGK Toán 10 Chân trời sáng tạo và các tài liệu tham khảo khác.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết ba đường conic trong mặt phẳng tọa độ. Chúc bạn học tốt!