Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 83, 84 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học toán online hiệu quả, tiết kiệm thời gian và đạt kết quả tốt nhất.
Bạn có nhận xét gì về giá của các cặp vectơ Quan sát Hình 8 và gọi tên các vectơ: Khẳng định sau đây đúng hay sai? Hãy giải thích. Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ
Bạn có nhận xét gì về giá của các cặp vectơ\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) trong Hình 6?
Lời giải chi tiết:
Ta có: giá của \(\overrightarrow {AB} \) là đường thẳng AB, giá của \(\overrightarrow {CD} \)là đường thẳng CD, và thấy rằng 2 đường thẳng này trùng nhau suy ra giá của 2 vecto này trùng nhau.
Tương tự ta thấy giá của cặp \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) song song với nhau.
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Phương pháp giải:
a) Xác định các vectơ có giá song song hoặc trùng với giá của vectơ x
b) Xác định các vectơ cùng phương, cùng chiều với vectơ a
c) Xác định các vectơ cùng phương, ngược chiều với vectơ u
Lời giải chi tiết:
a) Ta có:
Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)
Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)
Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)
b) Ta có:
Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)
c) Ta có:
Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)
Khẳng định sau đây đúng hay sai? Hãy giải thích.
Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)cùng hướng.
Phương pháp giải:
Thay đổi các vị trí của 3 điểm, kiểm tra hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) có cùng hướng hay không.
Lời giải chi tiết:
Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
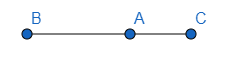
Khi A nằm giữa B và C thì hướng của vectơ \(\overrightarrow {AB} \) là từ phải sang trái, còn hướng của vectơ \(\overrightarrow {AC} \)là từ trái sang phải nên hai vectơ này là ngược hướng.
Bạn có nhận xét gì về giá của các cặp vectơ\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) trong Hình 6?
Lời giải chi tiết:
Ta có: giá của \(\overrightarrow {AB} \) là đường thẳng AB, giá của \(\overrightarrow {CD} \)là đường thẳng CD, và thấy rằng 2 đường thẳng này trùng nhau suy ra giá của 2 vecto này trùng nhau.
Tương tự ta thấy giá của cặp \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) song song với nhau.
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Phương pháp giải:
a) Xác định các vectơ có giá song song hoặc trùng với giá của vectơ x
b) Xác định các vectơ cùng phương, cùng chiều với vectơ a
c) Xác định các vectơ cùng phương, ngược chiều với vectơ u
Lời giải chi tiết:
a) Ta có:
Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)
Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)
Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)
b) Ta có:
Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)
c) Ta có:
Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)
Khẳng định sau đây đúng hay sai? Hãy giải thích.
Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)cùng hướng.
Phương pháp giải:
Thay đổi các vị trí của 3 điểm, kiểm tra hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) có cùng hướng hay không.
Lời giải chi tiết:
Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
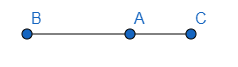
Khi A nằm giữa B và C thì hướng của vectơ \(\overrightarrow {AB} \) là từ phải sang trái, còn hướng của vectơ \(\overrightarrow {AC} \)là từ trái sang phải nên hai vectơ này là ngược hướng.
Mục 2 của chương trình Toán 10 tập 1 Chân trời sáng tạo tập trung vào các khái niệm cơ bản về tập hợp số, bao gồm tập số thực, các phép toán trên tập số thực, và các tính chất của chúng. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập trong mục 2 trang 83, 84 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm nhiều dạng bài khác nhau, từ các bài tập nhận biết, hiểu khái niệm đến các bài tập vận dụng, giải quyết vấn đề. Cụ thể:
Để xác định một số thuộc loại nào, các em cần nắm vững định nghĩa của từng loại số. Ví dụ:
Ví dụ: Số -2 là số nguyên, số 3.5 là số hữu tỉ, số π là số vô tỉ (và do đó là số thực).
Khi tính toán giá trị biểu thức, các em cần tuân thủ thứ tự thực hiện các phép toán: ngoặc, lũy thừa, nhân chia, cộng trừ. Lưu ý sử dụng đúng dấu ngoặc để đảm bảo kết quả chính xác.
Ví dụ: 2 + 3 * 4 = 2 + 12 = 14 (không phải là 20).
Để đơn giản hóa biểu thức, các em có thể sử dụng các tính chất của phép toán, chẳng hạn như:
Ví dụ: 2 * (3 + 4) = 2 * 3 + 2 * 4 = 6 + 8 = 14
Khi giải bài toán thực tế, các em cần đọc kỹ đề bài, xác định các dữ kiện và yêu cầu của bài toán. Sau đó, sử dụng kiến thức đã học để xây dựng mô hình toán học và giải bài toán.
Để học tốt môn Toán 10, các em cần:
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập mục 2 trang 83, 84 SGK Toán 10 tập 1 Chân trời sáng tạo, các em sẽ học tập hiệu quả và đạt kết quả tốt nhất. Chúc các em thành công!