Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 74 và 75 sách giáo khoa Toán 10 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Giải tam giác ABC trong các trường hợp sau:
Giải tam giác ABC trong các trường hợp sau:
a) \(a = 17,4;\widehat B = {44^o}30';\widehat C = {64^o}.\)
b) \(a = 10;b = 6;c = 8.\)
Phương pháp giải:
a) Áp dụng định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
b) Áp dụng hệ quả của định lí cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
Lời giải chi tiết:
a) Ta cần tính góc \(\widehat A\) và hai cạnh \(b,c.\)
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {44^o}30' - {64^o} = {71^o}30'.\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{17,4}}{{\sin {{71}^o}30'}} = \frac{b}{{\sin {{44}^o}30'}} = \frac{c}{{\sin {{64}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}b = \sin {44^o}30'.\frac{{17,4}}{{\sin {{71}^o}30'}} \approx 12,86\\c = \sin {64^o}.\frac{{17,4}}{{\sin {{71}^o}30'}} \approx 16,5\end{array} \right.\end{array}\)
b) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{6^2} + {8^2} - {{10}^2}}}{{2.6.8}} = 0;\cos B = \frac{{{{10}^2} + {8^2} - {6^2}}}{{2.10.8}} = \frac{4}{5}\\ \Rightarrow \widehat A = {90^o},\widehat B = {36^o}52'11,63''\\ \Rightarrow \widehat C = {53^o}7'48,37''\end{array}\)

Phương pháp giải:
Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Kí hiệu 3 điểm A, B, C như hình dưới.
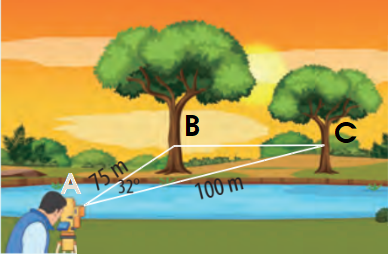
Áp dụng định lí cosin trong tam giác ABC, ta có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(b = AC = 100,c = AB = 75,\widehat A = {32^o}\)
\(\begin{array}{l} \Rightarrow {a^2} = {100^2} + {75^2} - 2.100.75.\cos {32^o} \approx 2904,28\\ \Leftrightarrow BC = a \approx 54\end{array}\)
Vậy khoảng cách giữa hai cây bên bờ sông là 54m.

Phương pháp giải:
Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Kí hiệu 3 điểm A, B, C như hình dưới.
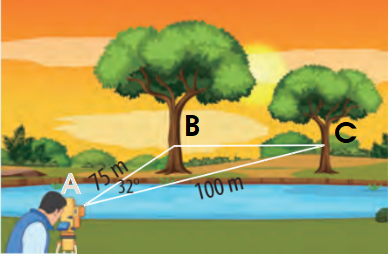
Áp dụng định lí cosin trong tam giác ABC, ta có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(b = AC = 100,c = AB = 75,\widehat A = {32^o}\)
\(\begin{array}{l} \Rightarrow {a^2} = {100^2} + {75^2} - 2.100.75.\cos {32^o} \approx 2904,28\\ \Leftrightarrow BC = a \approx 54\end{array}\)
Vậy khoảng cách giữa hai cây bên bờ sông là 54m.
Giải tam giác ABC trong các trường hợp sau:
a) \(a = 17,4;\widehat B = {44^o}30';\widehat C = {64^o}.\)
b) \(a = 10;b = 6;c = 8.\)
Phương pháp giải:
a) Áp dụng định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
b) Áp dụng hệ quả của định lí cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
Lời giải chi tiết:
a) Ta cần tính góc \(\widehat A\) và hai cạnh \(b,c.\)
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {44^o}30' - {64^o} = {71^o}30'.\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{17,4}}{{\sin {{71}^o}30'}} = \frac{b}{{\sin {{44}^o}30'}} = \frac{c}{{\sin {{64}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}b = \sin {44^o}30'.\frac{{17,4}}{{\sin {{71}^o}30'}} \approx 12,86\\c = \sin {64^o}.\frac{{17,4}}{{\sin {{71}^o}30'}} \approx 16,5\end{array} \right.\end{array}\)
b) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{6^2} + {8^2} - {{10}^2}}}{{2.6.8}} = 0;\cos B = \frac{{{{10}^2} + {8^2} - {6^2}}}{{2.10.8}} = \frac{4}{5}\\ \Rightarrow \widehat A = {90^o},\widehat B = {36^o}52'11,63''\\ \Rightarrow \widehat C = {53^o}7'48,37''\end{array}\)
Mục 1 của chương trình Toán 10 tập 1, Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp, các phép toán trên tập hợp, và các khái niệm cơ bản về số thực. Việc nắm vững những kiến thức này là nền tảng quan trọng cho việc học tập các chương tiếp theo.
Trang 74 và 75 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các bài tập vận dụng kiến thức về tập hợp, tập con, phép hợp, giao, hiệu, phần bù của tập hợp, và các tính chất của chúng. Các bài tập được thiết kế để giúp học sinh:
Bài 1 yêu cầu học sinh liệt kê các phần tử của một tập hợp cho trước. Để giải bài này, học sinh cần hiểu rõ định nghĩa của tập hợp và cách xác định các phần tử thuộc tập hợp đó. Ví dụ, nếu tập hợp A là tập hợp các số tự nhiên chẵn nhỏ hơn 10, thì các phần tử của A là: {0, 2, 4, 6, 8}.
Bài 2 yêu cầu học sinh xác định mối quan hệ giữa hai tập hợp, ví dụ như tập hợp nào là tập con của tập hợp nào, hai tập hợp có giao nhau hay không, v.v. Để giải bài này, học sinh cần hiểu rõ các khái niệm về tập con, tập hợp bằng nhau, và các phép toán trên tập hợp.
Bài 3 yêu cầu học sinh thực hiện các phép toán trên tập hợp, như phép hợp, giao, hiệu, phần bù của tập hợp. Để giải bài này, học sinh cần nắm vững các công thức và quy tắc thực hiện các phép toán trên tập hợp.
Bài 4 thường là các bài toán ứng dụng kiến thức về tập hợp vào giải quyết các bài toán thực tế. Để giải bài này, học sinh cần phân tích bài toán, xác định các tập hợp liên quan, và vận dụng các kiến thức đã học để tìm ra lời giải.
Dưới đây là lời giải chi tiết và hướng dẫn giải cho từng bài tập trong mục 1 trang 74, 75 SGK Toán 10 tập 1 Chân trời sáng tạo:
Để giải các bài tập về tập hợp nhanh chóng và hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Để hiểu sâu hơn về kiến thức về tập hợp, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 74, 75 SGK Toán 10 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!