Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 105, 106, 107 sách giáo khoa Toán 10 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Vinh và Hoa đo chiều dài trang bìa của một quyển số (Hình 2). Vinh đọc kết quả là 21 cm. Hãy tính độ dài đường chéo của một hình vuông có cạnh bằng 10 cm và xác định độ chính xác của kết quả tìm được. Một tấm bìa có dạng hình chữ nhật với kích thước được in như trong Hình 3. Vào năm 2015, các nhà khoa học trên thế giới ước lượng độ tuổi của vũ trụ là Hãy ước lượng sai số tương đối trong phép đo tuổi của vũ trụ và thời gian chạy của vận động viên
Vào năm 2015, các nhà khoa học trên thế giới ước lượng độ tuổi của vũ trụ là \(13\;799 \pm 21\) triệu năm.
Trọng tài bấm thời gian chạy 100 m của một vận động viên là \(10,3 \pm 0,1\) giây.
Theo bạn, trong hai phép đo trên, phép đo nào có độ chính xác cao hơn.
Phương pháp giải:
Cho \(\overline a = a + d\), nếu \(\frac{d}{{|a|}}\) càng nhỏ thì chất lượng của phép đo đạc (tính toán) càng cao.
Lời giải chi tiết:
Ta có: \(\frac{{21}}{{13799}} = 0,0015...\) và \(\frac{{0,1}}{{10,3}} = 0,0097...\)
\( \Rightarrow \frac{{21}}{{13799}} < \frac{{0,1}}{{10,3}}\) hay phép đo ước lượng độ tuổi của vũ trụ có độ chính xác cao hơn.
Cho biết \(1,41 < \sqrt 2 < 1,42.\) Hãy tính độ dài đường chéo của một hình vuông có cạnh bằng 10 cm và xác định độ chính xác của kết quả tìm được.
Phương pháp giải:
Bước 1: Xác định số gần đúng của \(\sqrt 2 \), tính độ dài đường chéo của hình vuông đó.
Bước 2: Tìm khoảng ước lượng, từ đó suy ra độ chính xác của kết quả.
Lời giải chi tiết:
Ta có: \(1,41 < \sqrt 2 < 1,42\) hay \(1,415 - 0,005 < \sqrt 2 < 1,415 + 0,005\)
\( \Rightarrow \) Số gần đúng của \(\sqrt 2 \) là 1,415 với độ chính xác 0,005
Khi đó: Độ dài đường chéo của hình vuông cạnh 10 cm là: \(10.1,415 = 14,15\;(cm)\)
Độ dài đúng là \(10\sqrt 2 \)cm, thỏa mãn: \(10.1,41 < 10\sqrt 2 < 10.1,42\) hay \(14,1 < 10\sqrt 2 < 14,2\)
Do đó \(14,1 - 14,15 < 10\sqrt 2 - 14,15 < 14,2 - 14,15\), tức là \(\left| {10\sqrt 2 - 14,15} \right| < 0,05.\)
Vậy kết quả 14,15 cm có độ chính xác là 0,05.
Hãy ước lượng sai số tương đối trong phép đo tuổi của vũ trụ và thời gian chạy của vận động viên ở Hoạt động khám phá 3.
Phương pháp giải:
Nếu \(\overline a = a + d\), sai số tương đối là \({\delta _a}\) và \({\delta _a} \le \frac{d}{{|a|}}\)
Lời giải chi tiết:
Trong phép đo tuổi của vũ trụ, ta có: \(d = 21;a = 13799\)
Sai số tương đối không vượt quá \(\frac{{21}}{{13799}} \approx 0,15\% \)
Trong phép đo thời gian chạy của vận động viên, ta có: \(d = 0,1;a = 10,3\)
Sai số tương đối không vượt quá \(\frac{{0,1}}{{10,3}} \approx 0,97\% \)
Vinh và Hoa đo chiều dài trang bìa của một quyển số (Hình 2). Vinh đọc kết quả là 21 cm. Hoa đọc kết quả là 20,7 cm. Kết quả của bạn nào có sai số nhỏ hơn?
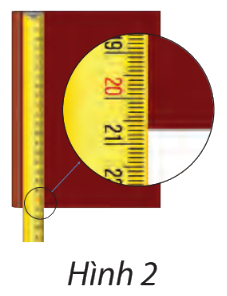
Lời giải chi tiết:
Quan sát Hình 2, ta thấy: Chiều dài trang bìa sổ gần tới vạch thứ 7 giữa số 20 và 21.
Do đó quyển sổ dài gần 20,7 cm.
Vậy kết quả của bạn Hoa có sai số nhỏ hơn.
Vinh và Hoa đo chiều dài trang bìa của một quyển số (Hình 2). Vinh đọc kết quả là 21 cm. Hoa đọc kết quả là 20,7 cm. Kết quả của bạn nào có sai số nhỏ hơn?
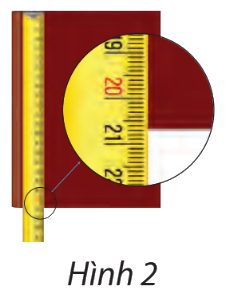
Lời giải chi tiết:
Quan sát Hình 2, ta thấy: Chiều dài trang bìa sổ gần tới vạch thứ 7 giữa số 20 và 21.
Do đó quyển sổ dài gần 20,7 cm.
Vậy kết quả của bạn Hoa có sai số nhỏ hơn.
Cho biết \(1,41 < \sqrt 2 < 1,42.\) Hãy tính độ dài đường chéo của một hình vuông có cạnh bằng 10 cm và xác định độ chính xác của kết quả tìm được.
Phương pháp giải:
Bước 1: Xác định số gần đúng của \(\sqrt 2 \), tính độ dài đường chéo của hình vuông đó.
Bước 2: Tìm khoảng ước lượng, từ đó suy ra độ chính xác của kết quả.
Lời giải chi tiết:
Ta có: \(1,41 < \sqrt 2 < 1,42\) hay \(1,415 - 0,005 < \sqrt 2 < 1,415 + 0,005\)
\( \Rightarrow \) Số gần đúng của \(\sqrt 2 \) là 1,415 với độ chính xác 0,005
Khi đó: Độ dài đường chéo của hình vuông cạnh 10 cm là: \(10.1,415 = 14,15\;(cm)\)
Độ dài đúng là \(10\sqrt 2 \)cm, thỏa mãn: \(10.1,41 < 10\sqrt 2 < 10.1,42\) hay \(14,1 < 10\sqrt 2 < 14,2\)
Do đó \(14,1 - 14,15 < 10\sqrt 2 - 14,15 < 14,2 - 14,15\), tức là \(\left| {10\sqrt 2 - 14,15} \right| < 0,05.\)
Vậy kết quả 14,15 cm có độ chính xác là 0,05.
Một tấm bìa có dạng hình chữ nhật với kích thước được in như trong Hình 3.
a) Hãy cho biết kích thước chiều dài và chiều rộng của tấm bìa nằm trong khoảng nà.
b) Tính diện tích của tấm bìa.

Phương pháp giải:
a) \(\overline a = a \pm d\) (hoặc \(a \pm d\)) thì có nghĩa là số đúng \(\overline a \) nằm trong đoạn \([a - d;a + d]\)
b)
Bước 1: Xác định chiều dài gần đúng và chiều rộng gần đúng.
Bước 2: Tính diện tích gần đúng và độ chính xác của kết quả đó.
Lời giải chi tiết:
a) Chiều rộng của tấm bìa là \(\overline R = 170 \pm 2mm\), nghĩa là chiều rộng gần đúng \(R = 170\)với độ chính xác \(d = 2\)
Suy ra kích thước chiều rộng nằm trong khoảng \(\left[ {170 - 2;170 + 2} \right]\) hay \(\left[ {168;{\rm{ }}172} \right].\)
Tương tự, chiều dài của tấm bìa là \(\overline D = 240 \pm 2mm\)
Vậy kích thước chiều dài nằm trong khoảng \(\left[ {240 - 2;240 + 2} \right]\) hay \([238;242]\)
b) Chiều rộng gần đúng là 170 mm, chiều dài gần đúng là 240 mm.
Khi đó, diện tích tấm bìa là \(S = 170.240 = 40800\;(m{m^2})\)
Diện tích đúng, kí hiệu \(\overline S \), của tấm bìa trên thỏa mãn:
\(168.238 < \overline S < 172.242 \Leftrightarrow 39984 < \overline S < 41624\)
Do đó \(39984 - 40800 < \overline S - 40800 < 41624 - 40800\) hay \( - 816 < \overline S - S < 824 \Rightarrow \left| {\overline S - S} \right| < 824\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)
Cách 2:
Diện tích tấm bìa là:
\(\overline S = \left( {170 \pm 2} \right)\left( {240 \pm 2} \right) = 170.240 \pm \left( {170.2 + 240.2 + 2.2} \right) = 40800 \pm 824\left( {m{m^2}} \right)\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)
Vào năm 2015, các nhà khoa học trên thế giới ước lượng độ tuổi của vũ trụ là \(13\;799 \pm 21\) triệu năm.
Trọng tài bấm thời gian chạy 100 m của một vận động viên là \(10,3 \pm 0,1\) giây.
Theo bạn, trong hai phép đo trên, phép đo nào có độ chính xác cao hơn.
Phương pháp giải:
Cho \(\overline a = a + d\), nếu \(\frac{d}{{|a|}}\) càng nhỏ thì chất lượng của phép đo đạc (tính toán) càng cao.
Lời giải chi tiết:
Ta có: \(\frac{{21}}{{13799}} = 0,0015...\) và \(\frac{{0,1}}{{10,3}} = 0,0097...\)
\( \Rightarrow \frac{{21}}{{13799}} < \frac{{0,1}}{{10,3}}\) hay phép đo ước lượng độ tuổi của vũ trụ có độ chính xác cao hơn.
Hãy ước lượng sai số tương đối trong phép đo tuổi của vũ trụ và thời gian chạy của vận động viên ở Hoạt động khám phá 3.
Phương pháp giải:
Nếu \(\overline a = a + d\), sai số tương đối là \({\delta _a}\) và \({\delta _a} \le \frac{d}{{|a|}}\)
Lời giải chi tiết:
Trong phép đo tuổi của vũ trụ, ta có: \(d = 21;a = 13799\)
Sai số tương đối không vượt quá \(\frac{{21}}{{13799}} \approx 0,15\% \)
Trong phép đo thời gian chạy của vận động viên, ta có: \(d = 0,1;a = 10,3\)
Sai số tương đối không vượt quá \(\frac{{0,1}}{{10,3}} \approx 0,97\% \)
Một tấm bìa có dạng hình chữ nhật với kích thước được in như trong Hình 3.
a) Hãy cho biết kích thước chiều dài và chiều rộng của tấm bìa nằm trong khoảng nà.
b) Tính diện tích của tấm bìa.

Phương pháp giải:
a) \(\overline a = a \pm d\) (hoặc \(a \pm d\)) thì có nghĩa là số đúng \(\overline a \) nằm trong đoạn \([a - d;a + d]\)
b)
Bước 1: Xác định chiều dài gần đúng và chiều rộng gần đúng.
Bước 2: Tính diện tích gần đúng và độ chính xác của kết quả đó.
Lời giải chi tiết:
a) Chiều rộng của tấm bìa là \(\overline R = 170 \pm 2mm\), nghĩa là chiều rộng gần đúng \(R = 170\)với độ chính xác \(d = 2\)
Suy ra kích thước chiều rộng nằm trong khoảng \(\left[ {170 - 2;170 + 2} \right]\) hay \(\left[ {168;{\rm{ }}172} \right].\)
Tương tự, chiều dài của tấm bìa là \(\overline D = 240 \pm 2mm\)
Vậy kích thước chiều dài nằm trong khoảng \(\left[ {240 - 2;240 + 2} \right]\) hay \([238;242]\)
b) Chiều rộng gần đúng là 170 mm, chiều dài gần đúng là 240 mm.
Khi đó, diện tích tấm bìa là \(S = 170.240 = 40800\;(m{m^2})\)
Diện tích đúng, kí hiệu \(\overline S \), của tấm bìa trên thỏa mãn:
\(168.238 < \overline S < 172.242 \Leftrightarrow 39984 < \overline S < 41624\)
Do đó \(39984 - 40800 < \overline S - 40800 < 41624 - 40800\) hay \( - 816 < \overline S - S < 824 \Rightarrow \left| {\overline S - S} \right| < 824\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)
Cách 2:
Diện tích tấm bìa là:
\(\overline S = \left( {170 \pm 2} \right)\left( {240 \pm 2} \right) = 170.240 \pm \left( {170.2 + 240.2 + 2.2} \right) = 40800 \pm 824\left( {m{m^2}} \right)\)
Vậy diện tích tấm bìa là \(40800 \pm 824\;\left( {m{m^2}} \right)\)
Mục 2 của chương trình Toán 10 tập 1, Chân trời sáng tạo thường tập trung vào các khái niệm và ứng dụng của vectơ trong mặt phẳng. Các bài tập trong trang 105, 106, 107 thường xoay quanh việc xác định tọa độ vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực), và ứng dụng các kiến thức này để giải quyết các bài toán hình học cơ bản.
Bài tập này yêu cầu học sinh xác định tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ đó. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ vectơ: Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ (xB - xA, yB - yA).
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ vectơ. Để giải bài tập này, học sinh cần nắm vững quy tắc cộng, trừ vectơ: Nếu a(xa, ya) và b(xb, yb) thì a + b = (xa + xb, ya + yb) và a - b = (xa - xb, ya - yb).
Bài tập này yêu cầu học sinh thực hiện phép nhân vectơ với một số thực. Để giải bài tập này, học sinh cần nắm vững quy tắc nhân vectơ với một số thực: Nếu a(xa, ya) và k là một số thực thì k.a = (k.xa, k.ya).
Bài tập này yêu cầu học sinh ứng dụng các kiến thức về vectơ để giải quyết các bài toán hình học, ví dụ như chứng minh hai vectơ cùng phương, tìm tọa độ trung điểm của đoạn thẳng, hoặc chứng minh ba điểm thẳng hàng. Để giải bài tập này, học sinh cần kết hợp kiến thức về vectơ với các kiến thức hình học đã học.
Ví dụ: Cho A(1, 2) và B(3, 4). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ (3 - 1, 4 - 2) = (2, 2).
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tự giải thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn học sinh khác.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 105, 106, 107 SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!