Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 15 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Cho các định lí: P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Q: “Nếu a <b thì a + c < b + c” (a,b,c thuộc R). a) Chỉ ra giả thiết và kết luận của mỗi định lí. b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”. c) Mệnh đề đảo của mỗi định lí đó có là định lí không?
Đề bài
Cho các định lí:
P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.
Q: “Nếu \(a < b\) thì \(a + c < b + c\)” (\(a,b,c \in \mathbb{R}\)).
a) Chỉ ra giả thiết và kết luận của mỗi định lí.
b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.
c) Mệnh đề đảo của mỗi định lí đó có là định lí không?
Phương pháp giải - Xem chi tiết
+) Khi mệnh đề \(R \Rightarrow T\) là định lí, ta nói:
R là giả thiết, T là kết luận
R là điều kiện đủ để có T
T là điều kiện cần để có R
+) Mệnh đề đảo của mệnh đề \(R \Rightarrow T\) là mệnh đề \(T \Rightarrow R\).
Lời giải chi tiết
a)
Mệnh đề P có dạng \(R \Rightarrow T\)với R: “Hai tam giác bằng nhau” và T: “Diện tích của hai tam giác bằng nhau”
Giả thiết là mệnh đề R: “Hai tam giác bằng nhau”
Kết luận là mệnh đề T: “Diện tích của hai tam giác bằng nhau”
Mệnh đề Q có dạng \(A \Rightarrow B\)với A: “\(a < b\)” và B: “\(a + c < b + c\)”
Giả thiết là mệnh đề A: “\(a < b\)”
Kết luận là mệnh đề B: “\(a + c < b + c\)”
b)
+) Mệnh đề P có thể phát biểu lại như sau:
Hai tam giác bằng nhau là điều kiện đủ để có diện tích của chúng bằng nhau.
Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác bằng nhau.
+) Mệnh đề Q có thể phát biểu lại như sau:
\(a < b\) là điều kiện đủ để có \(a + c < b + c\).
\(a + c < b + c\)là điều kiện cần để có \(a < b\).
c)
Mệnh đề đảo của mệnh đề P có dạng \(T \Rightarrow R\), phát biểu là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.
Mệnh đề này sai nên không là định lí.
Chẳng hạn: Tam giác ABC và tam giác DEF, có diện tích bằng nhau nhưng hai tam giác không bằng nhau.
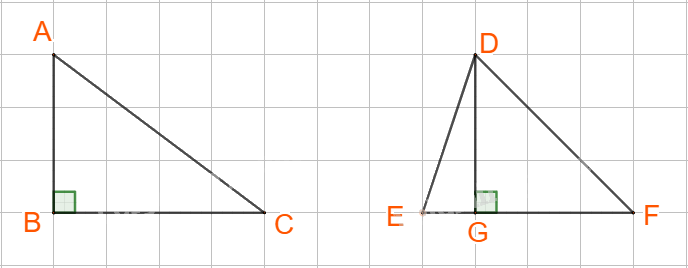
Mệnh đề đảo của mệnh đề Q có dạng \(B \Rightarrow A\), phát biểu là: “Nếu \(a + c < b + c\)thì \(a < b\)”.
Mệnh đề này đúng nên nó cũng là định lí.
Bài 4 trang 15 SGK Toán 10 tập 1 Chân trời sáng tạo thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán trên tập hợp, bao gồm hợp, giao, hiệu và phần bù của tập hợp để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và quy tắc này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 10.
Bài 4 trang 15 SGK Toán 10 tập 1 Chân trời sáng tạo thường bao gồm các câu hỏi yêu cầu:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập và đưa ra lời giải chi tiết:
...
...
...
Để giải quyết bài 4 trang 15 SGK Toán 10 tập 1 Chân trời sáng tạo một cách hiệu quả, các em cần nắm vững các khái niệm sau:
Dưới đây là một số mẹo giúp các em giải bài tập về tập hợp một cách dễ dàng hơn:
Để củng cố kiến thức về tập hợp, các em có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 15 SGK Toán 10 tập 1 Chân trời sáng tạo là một bài tập quan trọng giúp các em nắm vững kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong quá trình học tập môn Toán 10.