Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài 8 trang 79 một cách hiệu quả.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy tiên tiến.
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là
Đề bài
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là \(2,{1^ \circ }.\)
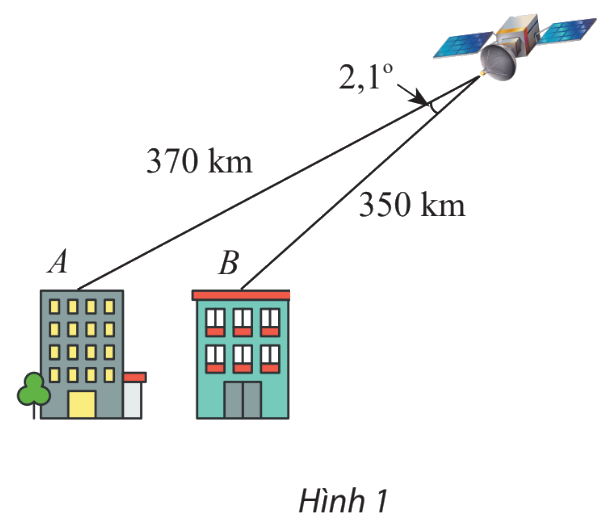
Phương pháp giải - Xem chi tiết
Áp dụng định lí cosin: \(A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\)
Lời giải chi tiết
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\\ \Rightarrow AB \approx 23,96\;(km)\end{array}\)
Vậy khoảng cách giữa hai tòa nhà là 23,96 km.
Bài 8 trang 79 SGK Toán 10 tập 1 Chân trời sáng tạo thuộc chương trình học về Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là phép cộng, trừ vectơ và phép nhân vectơ với một số thực để giải quyết các bài toán liên quan đến hình học và vật lý.
Bài 8 bao gồm các câu hỏi và bài tập khác nhau, tập trung vào việc:
Cho hai vectơ a = (2; -1) và b = (-3; 4). Tính a + b và a - b.
Lời giải:
a + b = (2 + (-3); -1 + 4) = (-1; 3)
a - b = (2 - (-3); -1 - 4) = (5; -5)
Cho vectơ u = (1; 2) và số thực k = 3. Tính ku.
Lời giải:
ku = 3(1; 2) = (3 * 1; 3 * 2) = (3; 6)
Cho ba điểm A(1; 2), B(3; 4), C(5; 6). Chứng minh rằng A, B, C thẳng hàng.
Lời giải:
Ta có vectơ AB = (3 - 1; 4 - 2) = (2; 2)
Vectơ AC = (5 - 1; 6 - 2) = (4; 4)
Vì AC = 2AB nên vectơ AC và AB cùng phương. Hơn nữa, A, B, C cùng nằm trên đường thẳng đi qua A. Do đó, A, B, C thẳng hàng.
Vectơ có rất nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn đã hiểu rõ cách giải bài 8 trang 79 SGK Toán 10 tập 1 Chân trời sáng tạo. Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác trong môn Toán nhé!