Trong chương trình Toán 10 CTST, việc hiểu rõ các số đặc trưng đo mức độ phân tán của mẫu số liệu là vô cùng quan trọng. Chúng giúp ta đánh giá được sự biến động, độ rộng của tập dữ liệu.
giaitoan.edu.vn cung cấp bài học chi tiết, dễ hiểu về các khái niệm như khoảng biến thiên, phương sai, độ lệch chuẩn, giúp bạn nắm vững kiến thức nền tảng và áp dụng vào giải bài tập một cách hiệu quả.
Các số đặc trưng đo xu thế trung tâm của mẫu số liệu
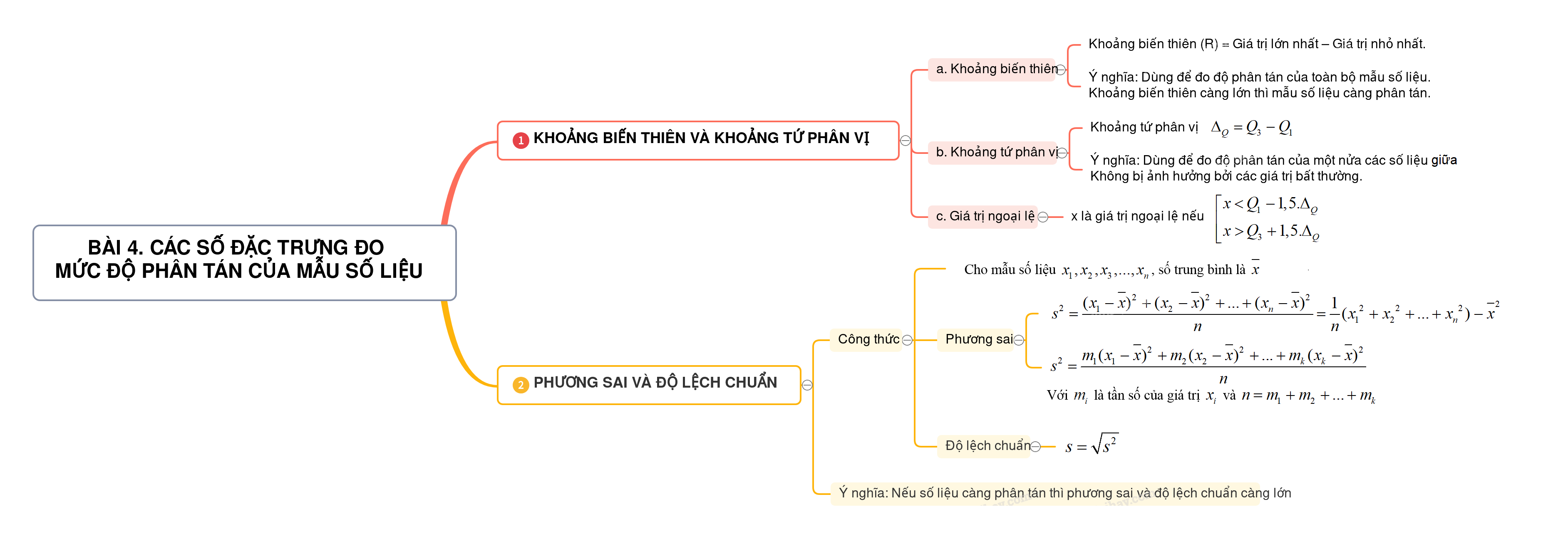
1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ
a. Khoảng biến thiên
Khoảng biến thiên (R) = Giá trị lớn nhất – Giá trị nhỏ nhất.
Ý nghĩa: Dùng để đo độ phân tán của toàn bộ mẫu số liệu: Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.
b. Khoảng tứ phân vị
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Ý nghĩa: Dùng để đo độ phân tán của một nửa các số liệu có giá trị thuộc đoạn từ \({Q_1}\) đến \({Q_3}\) trong mẫu.
Không bị ảnh hưởng bởi các giá trị bất thường.
c. Giá trị ngoại lệ
\(x\) là giá trị ngoại lệ nếu \(\left[ \begin{array}{l}x < {Q_1} - 1,5.{\Delta _Q}\\x > {Q_3} + 1,5.{\Delta _Q}\end{array} \right.\)
2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN
Cho mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\), số trung bình là \(\overline x \)
+ Phương sai: \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n} = \frac{1}{n}({x_1}^2 + {x_2}^2 + ... + {x_n}^2) - {\overline x ^2}\)
+ Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)
Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn
Chú ý: Phương sai của mẫu số liệu cho dạng bảng tần số:
\({s^2} = \frac{{{m_1}{{({x_1} - \overline x )}^2} + {m_2}{{({x_2} - \overline x )}^2} + ... + {m_k}{{({x_k} - \overline x )}^2}}}{n}\)
Với \({m_i}\) là tần số của giá trị \({x_i}\) và \(n = {m_1} + {m_2} + ... + {m_k}\)
Trong thống kê, việc mô tả một tập dữ liệu không chỉ dừng lại ở việc tìm các giá trị trung tâm như trung bình cộng, trung vị, mốt. Để hiểu rõ hơn về sự phân tán của dữ liệu, chúng ta cần sử dụng các số đặc trưng đo mức độ phân tán. Bài viết này sẽ trình bày chi tiết về các số đặc trưng này theo chương trình SGK Toán 10 CTST.
Khoảng biến thiên là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong một mẫu số liệu. Nó cho biết phạm vi mà dữ liệu trải rộng. Công thức tính khoảng biến thiên (R) như sau:
R = Xmax - Xmin
Trong đó:
Ví dụ: Cho mẫu số liệu: 2, 4, 6, 8, 10. Khoảng biến thiên là 10 - 2 = 8.
Phương sai đo lường mức độ phân tán của các giá trị trong một mẫu số liệu so với giá trị trung bình. Phương sai được ký hiệu là σ2 (cho tổng thể) hoặc s2 (cho mẫu). Công thức tính phương sai mẫu (s2) như sau:
s2 = ∑(xi - x̄)2 / (n - 1)
Trong đó:
Ví dụ: Cho mẫu số liệu: 2, 4, 6, 8, 10. Giá trị trung bình x̄ = (2+4+6+8+10)/5 = 6. Phương sai là:
s2 = [(2-6)2 + (4-6)2 + (6-6)2 + (8-6)2 + (10-6)2] / (5-1) = (16 + 4 + 0 + 4 + 16) / 4 = 40 / 4 = 10
Độ lệch chuẩn là căn bậc hai của phương sai. Nó cũng đo lường mức độ phân tán của các giá trị trong một mẫu số liệu so với giá trị trung bình, nhưng có đơn vị đo giống với dữ liệu gốc. Độ lệch chuẩn được ký hiệu là σ (cho tổng thể) hoặc s (cho mẫu). Công thức tính độ lệch chuẩn mẫu (s) như sau:
s = √s2
Ví dụ: Sử dụng kết quả phương sai ở trên (s2 = 10), độ lệch chuẩn là s = √10 ≈ 3.16.
Khoảng biến thiên cho biết phạm vi của dữ liệu. Phương sai và độ lệch chuẩn cho biết mức độ tập trung của dữ liệu xung quanh giá trị trung bình. Độ lệch chuẩn càng lớn, dữ liệu càng phân tán; độ lệch chuẩn càng nhỏ, dữ liệu càng tập trung.
Cho bảng số liệu thống kê về chiều cao của 10 học sinh (đơn vị cm):
| STT | Chiều cao (cm) |
|---|---|
| 1 | 155 |
| 2 | 160 |
| 3 | 162 |
| 4 | 165 |
| 5 | 168 |
| 6 | 170 |
| 7 | 172 |
| 8 | 175 |
| 9 | 178 |
| 10 | 180 |
Tính khoảng biến thiên, phương sai và độ lệch chuẩn của mẫu số liệu này.
Giải:
Việc nắm vững lý thuyết và cách tính các số đặc trưng đo mức độ phân tán là nền tảng quan trọng để phân tích và hiểu rõ hơn về dữ liệu thống kê. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về chủ đề này trong chương trình SGK Toán 10 CTST.