Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
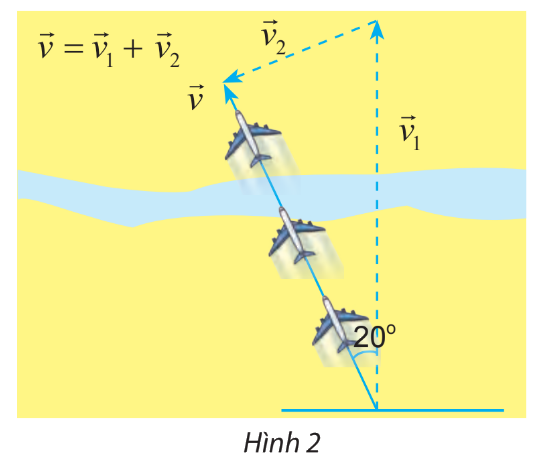
Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ 45m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc 20 về phía tây bắc (hình 2). Tính tốc độ của gió
Đề bài
Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ \(45\)m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc \(20^\circ \) về phía tây bắc (hình 2). Tính tốc độ của gió
Phương pháp giải - Xem chi tiết
Bước 1: Dựa vào hình 2 xác định các vectơ tương ứng với vận tốc của máy bay, vận tốc so với mặt đất
Bước 2: Dựa vào mối liên hệ giữa các vectơ đã cho \(\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \) xác định vectơ tương ứng với vận tốc gió
Bước 3: Áp dụng định lý cosin tìm tốc độ của gió
Lời giải chi tiết
Từ giả thiết ta có:
+) Vectơ tương ứng với vận tốc máy bay là vectơ \(\overrightarrow {{v_1}} \)
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ \(\overrightarrow v \)
+) Vectơ tương ứng với vận tốc gió là vectơ \(\overrightarrow {{v_2}} \)
Ta có : \(\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ \)
Áp dụng định lý cosin ta có:
\(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)} \)
\( = \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16\) (m/s)
Vậy tốc độ của gió gần bằng 16 m/s
Bài 9 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và đặc biệt là ứng dụng của vectơ trong việc chứng minh các tính chất hình học.
Bài 9 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích chi tiết từng phần của bài tập. (Lưu ý: Vì bài tập cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa về cách giải một bài tập tương tự.)
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng vectơ AM = (1/2) vectơ AB + vectơ AC.
Lời giải:
vectơ AM = vectơ AB + (1/2) vectơ AB = (3/2) vectơ AB
vectơ AC = vectơ AB + vectơ BC = vectơ AB + vectơ AD
Do đó, (1/2) vectơ AB + vectơ AC = (1/2) vectơ AB + vectơ AB + vectơ AD = (3/2) vectơ AB + vectơ AD
vectơ AM = vectơ AB + vectơ BM = vectơ AB + (1/2) vectơ BC = vectơ AB + (1/2) vectơ AD
vectơ AC = vectơ AB + vectơ BC = vectơ AB + vectơ AD
Suy ra vectơ AD = vectơ AC - vectơ AB
Thay vào vectơ AM, ta có: vectơ AM = vectơ AB + (1/2) (vectơ AC - vectơ AB) = (1/2) vectơ AB + (1/2) vectơ AC
Ngoài SGK Toán 10 tập 1 – Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập vectơ trên, các em sẽ tự tin hơn khi giải bài 9 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tập tốt!