Bài 6 trang 56 SGK Toán 10 tập 1 thuộc chương trình Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 56 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Vẽ đồ thị các hàm số sau:
a) \(y = 2{x^2} + 4x - 1\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0)
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
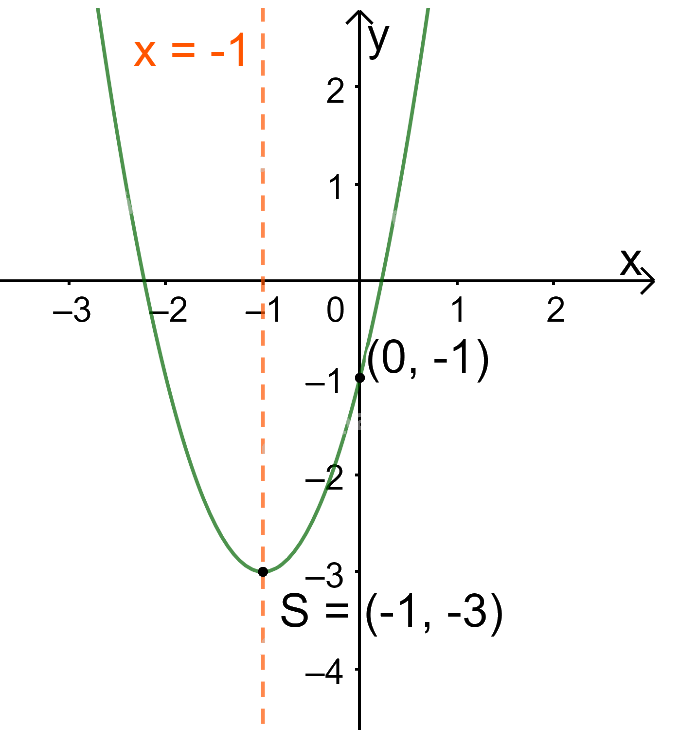
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
b) \(y = - {x^2} + 2x + 3\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay xuống dưới (a=-1<0).
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
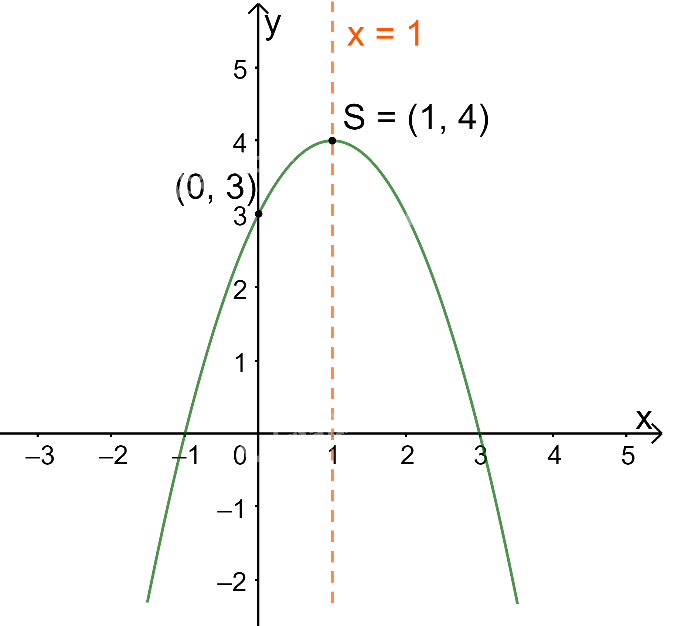
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
d) \(y = 2{x^2} - 5\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0), quay xuống dưới nếu a<0.
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
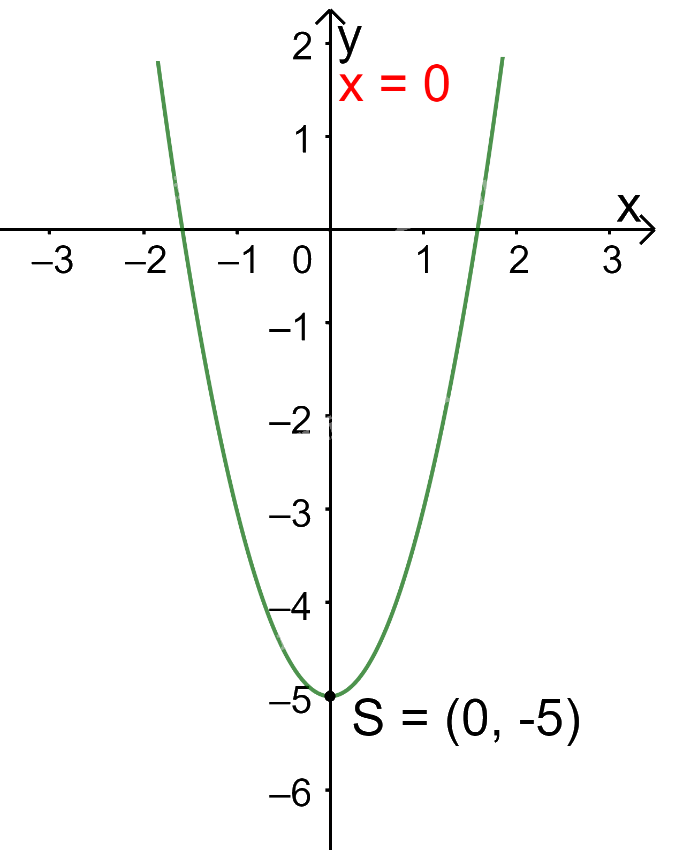
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.
Vẽ đồ thị các hàm số sau:
a) \(y = 2{x^2} + 4x - 1\)
b) \(y = - {x^2} + 2x + 3\)
c) \(y = - 3{x^2} + 6x\)
d) \(y = 2{x^2} - 5\)
a) \(y = 2{x^2} + 4x - 1\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0)
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
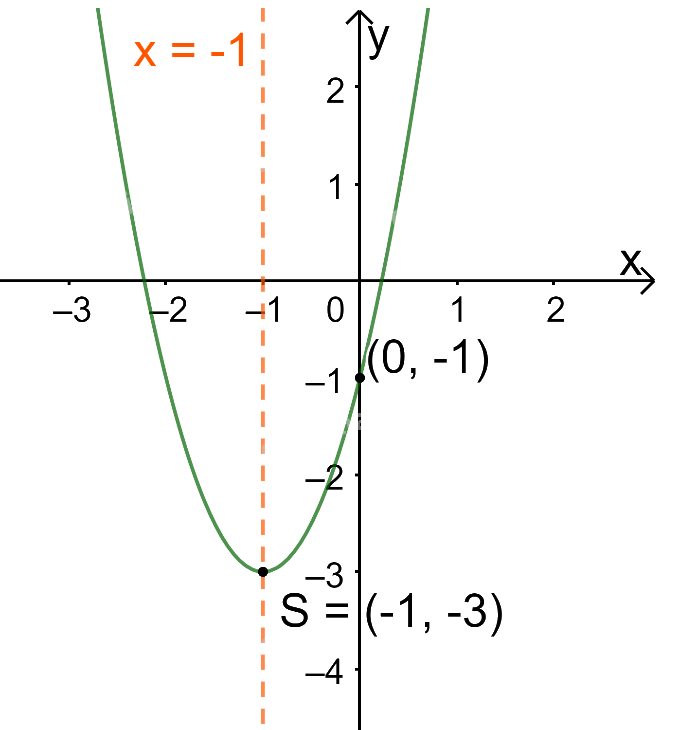
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
b) \(y = - {x^2} + 2x + 3\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay xuống dưới (a=-1<0).
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
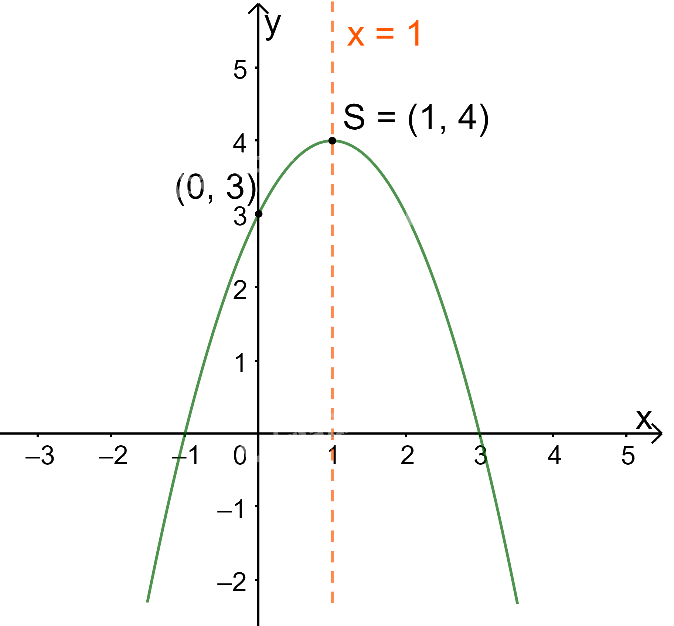
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
c) \(y = - 3{x^2} + 6x\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0), quay xuống dưới nếu a<0.
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
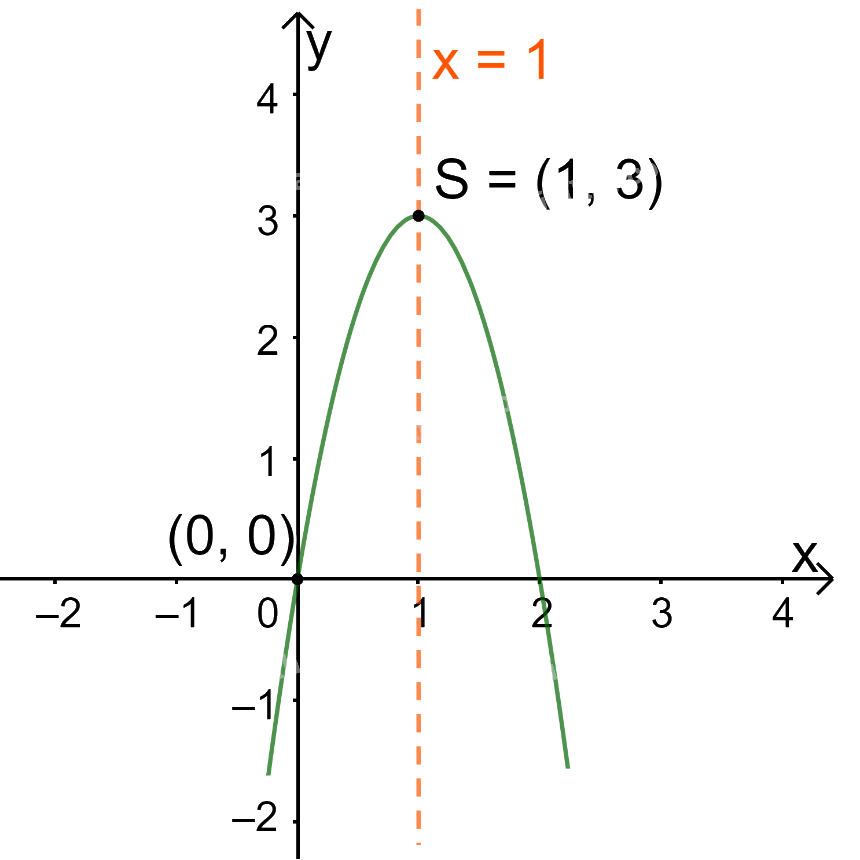
d) \(y = 2{x^2} - 5\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0), quay xuống dưới nếu a<0.
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
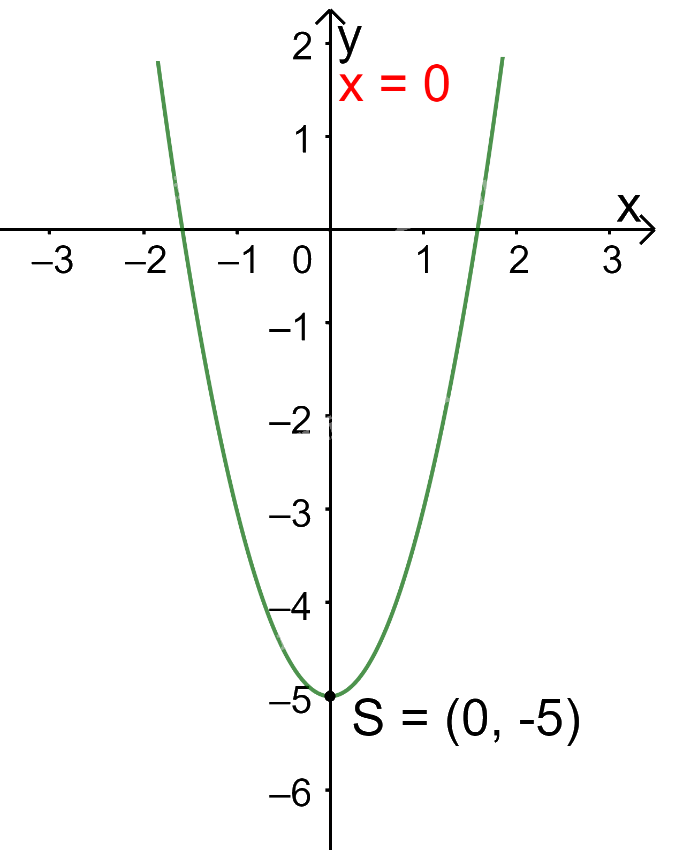
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.
c) \(y = - 3{x^2} + 6x\)
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0), quay xuống dưới nếu a<0.
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
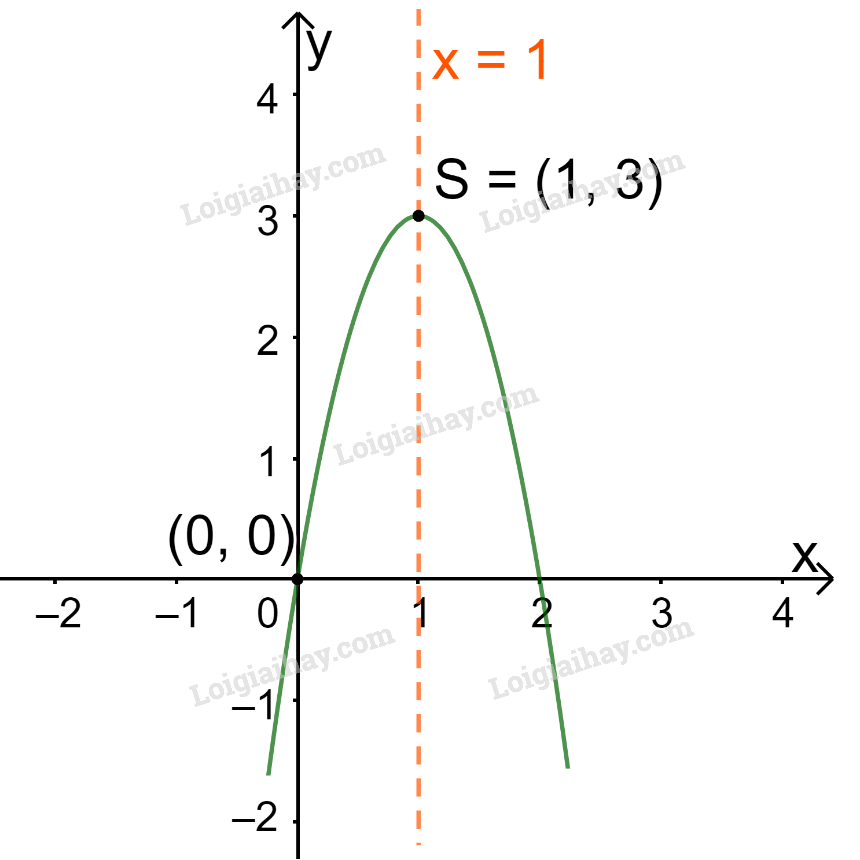
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
Bài 6 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập thuộc chương 2: Tập hợp và các phép toán trên tập hợp. Bài tập này tập trung vào việc xác định các tập hợp con, tập hợp bằng nhau, và thực hiện các phép toán hợp, giao, hiệu của các tập hợp. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học các chương trình Toán học nâng cao hơn.
Bài 6 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo thường bao gồm các câu hỏi yêu cầu học sinh:
Để giải bài tập về tập hợp hiệu quả, học sinh cần:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng câu hỏi cụ thể trong bài tập. Dưới đây là một ví dụ minh họa:
Cho hai tập hợp A = {1, 2, 3} và B = {2, 3, 4}. Hãy tìm:
Lời giải:
Ngoài các bài tập cơ bản về phép toán trên tập hợp, bài 6 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo còn có thể xuất hiện các dạng bài tập sau:
Để giải nhanh các bài tập về tập hợp, học sinh có thể sử dụng các mẹo sau:
Để học tập và ôn luyện kiến thức về tập hợp, học sinh có thể tham khảo các tài liệu sau:
Bài 6 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về tập hợp và các phép toán trên tập hợp. Bằng cách nắm vững các định nghĩa, phương pháp giải và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.