Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 18, 19, 20 sách giáo khoa Toán 10 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không? Viết tất cả các tập con của tập hợp A = { a;b} .
Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.
a) \(A = \{ - 1;1\} \) và \(B = \{ - 1;0;1;2\} \)
b) \(A = \mathbb{N}\) và \(B = \mathbb{Z}\)
c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.
d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.
Lời giải chi tiết:
a) Có vì \( - 1 \in B,\;1 \in B\).
b) Có vì các số tự nhiên cũng là số nguyên.
c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.
d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?
a) \(A = \{ - \sqrt 3 ;\sqrt 3 \} \) và \(B = \{ x \in \mathbb{R}|{x^2} - 3 = 0\} \)
b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;
c) \(E = \{ x \in \mathbb{N}|x\) là ước của 12\(\} \) và \(F = \{ x \in \mathbb{N}|x\) là ước của 24\(\} .\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Phương pháp giải:
\(A \subset B\) nếu mọi phần tử của A đều là phần tử của B.
\(A = B\) nếu \(A \subset B\) và \(B \subset A\)
Lời giải chi tiết:
a) A là tập con củ B vì:
\( - \sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3 \in B\)
\(\sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3 \in B\)
Lại có: \({x^2} - 3 = 0 \Leftrightarrow x = \pm \sqrt 3 \) nên \(B = \{ - \sqrt 3 ;\sqrt 3 \} \).
Vậy A = B.
b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.
\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.
c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.
\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Lời giải chi tiết:
Các tập con của tập hợp A là:
+) Tập con có 0 phần tử: \(\emptyset \) (tập hợp rỗng)
+) Tập hợp con có 1 phần tử: {a}, {b}
+) Tập hợp con có 2 phần tử: \(A = \{ a;b\} .\)
Chú ý
+) Mọi tập hợp A đều có 2 tập con là: \(\emptyset \) và A.
Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)
Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
Lời giải chi tiết:
+) Biểu diễn: \(A \subset B\)
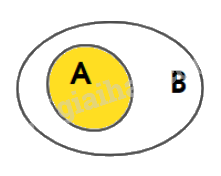
+) Sau đó, biểu diễn: \(B \subset C\)
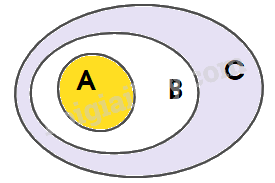
Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)
Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.
a) \(A = \{ - 1;1\} \) và \(B = \{ - 1;0;1;2\} \)
b) \(A = \mathbb{N}\) và \(B = \mathbb{Z}\)
c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.
d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.
Lời giải chi tiết:
a) Có vì \( - 1 \in B,\;1 \in B\).
b) Có vì các số tự nhiên cũng là số nguyên.
c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.
d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?
a) \(A = \{ - \sqrt 3 ;\sqrt 3 \} \) và \(B = \{ x \in \mathbb{R}|{x^2} - 3 = 0\} \)
b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;
c) \(E = \{ x \in \mathbb{N}|x\) là ước của 12\(\} \) và \(F = \{ x \in \mathbb{N}|x\) là ước của 24\(\} .\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Phương pháp giải:
\(A \subset B\) nếu mọi phần tử của A đều là phần tử của B.
\(A = B\) nếu \(A \subset B\) và \(B \subset A\)
Lời giải chi tiết:
a) A là tập con củ B vì:
\( - \sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3 \in B\)
\(\sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3 \in B\)
Lại có: \({x^2} - 3 = 0 \Leftrightarrow x = \pm \sqrt 3 \) nên \(B = \{ - \sqrt 3 ;\sqrt 3 \} \).
Vậy A = B.
b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.
\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.
c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.
\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Lời giải chi tiết:
Các tập con của tập hợp A là:
+) Tập con có 0 phần tử: \(\emptyset \) (tập hợp rỗng)
+) Tập hợp con có 1 phần tử: {a}, {b}
+) Tập hợp con có 2 phần tử: \(A = \{ a;b\} .\)
Chú ý
+) Mọi tập hợp A đều có 2 tập con là: \(\emptyset \) và A.
Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)
Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
Lời giải chi tiết:
+) Biểu diễn: \(A \subset B\)
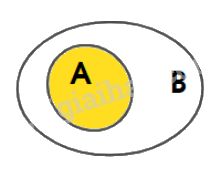
+) Sau đó, biểu diễn: \(B \subset C\)
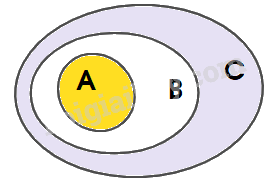
Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)
Mục 2 của chương trình Toán 10 tập 1 - Chân trời sáng tạo tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên. Bài viết này sẽ đi sâu vào từng bài tập trong mục 2, trang 18, 19, 20, cung cấp lời giải chi tiết, dễ hiểu, và các ví dụ minh họa.
Bài tập này yêu cầu học sinh xác định các phần tử thuộc một tập hợp cho trước. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của tập hợp và cách xác định các phần tử của tập hợp. Ví dụ, nếu tập hợp A chứa các số tự nhiên chẵn nhỏ hơn 10, thì các phần tử của tập hợp A là: {0, 2, 4, 6, 8}.
Bài tập này yêu cầu học sinh xác định xem một mệnh đề có đúng hay sai. Để giải bài tập này, học sinh cần hiểu rõ các khái niệm về mệnh đề, giá trị chân lý của mệnh đề, và các phép toán logic. Ví dụ, mệnh đề “2 + 2 = 4” là một mệnh đề đúng, trong khi mệnh đề “2 + 2 = 5” là một mệnh đề sai.
Bài tập này yêu cầu học sinh thực hiện các phép toán trên tập hợp, như hợp, giao, hiệu, và phần bù. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của các phép toán trên tập hợp và cách thực hiện chúng. Ví dụ, nếu A = {1, 2, 3} và B = {2, 3, 4}, thì A ∪ B = {1, 2, 3, 4} và A ∩ B = {2, 3}.
Bài tập này yêu cầu học sinh chứng minh các đẳng thức tập hợp. Để giải bài tập này, học sinh cần sử dụng các tính chất của các phép toán trên tập hợp và các quy tắc logic. Ví dụ, để chứng minh A ∪ B = B ∪ A, ta có thể sử dụng tính chất giao hoán của phép hợp.
Ví dụ 1: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B và A ∩ B.
Giải:
Ví dụ 2: Cho A = {a, b, c} và B = {b, c, d}. Tìm A \ B và B \ A.
Giải:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải các bài tập trong mục 2 trang 18, 19, 20 SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!