Bài 11 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 11 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một xe goòng được kéo bởi một lực F có độ lớn là là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài là 200 m.
Đề bài
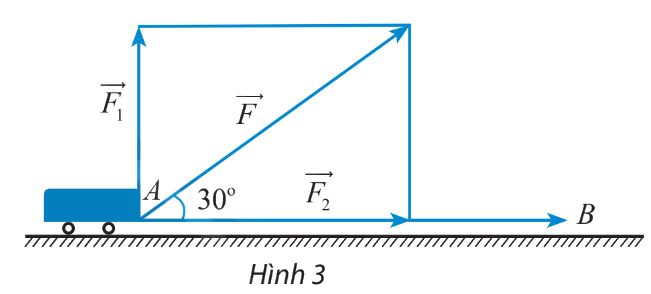
Một xe goòng được kéo bởi một lực \(\overrightarrow F \) có độ lớn là là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài là 200 m. Cho biết góc giữa lực \(\overrightarrow F \) và \(\overrightarrow {AB} \) là \(30^\circ \) và \(\overrightarrow F \) được phân tích thành 2 lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hình 3). Tính công sinh ra bởi các lực \(\overrightarrow F ,\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng các tính chất trong tam giác vuông xác định độ lớn của các lực.
Bước 2: Xác định góc giữa các lực và hướng dịch chuyển.
Bước 3: Sử dụng công thức \(A = \overrightarrow F .\overrightarrow d \) (với \(\overrightarrow d \) là vectơ thể hiện độ dịch chuyển và quãng đường mà vật đi được).
Lời giải chi tiết
Ta xác định được các độ lớn:
\(\left| {\overrightarrow F } \right| = 50,\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow F } \right|\cos 30^\circ = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 ,\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right|.\sin 30^\circ = 50.\frac{1}{2} = 25\) (N)
Dựa vào hình vẽ ta có: \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 30^\circ ,\left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 90^\circ ,\left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 0^\circ \)
Áp dụng công thức tính công sinh ra bởi lực \(A = \overrightarrow F .\overrightarrow d \) ta có:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 50.200.\cos 30^\circ = 5000\sqrt 3 (J)\)
\({A_1} = \overrightarrow {{F_1}} .\overrightarrow d = \left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 25.200.\cos 90^\circ = 0 (J)\)
\({A_2} = \overrightarrow {{F_2}} .\overrightarrow d = \left| {\overrightarrow {{F_2}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 25\sqrt 3 .200.\cos 0^\circ = 5000\sqrt 3 (J)\)
Bài 11 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Phương pháp giải bài tập vectơ thường bao gồm các bước sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD)).
Lời giải:
Bước 1: Xác định các vectơ liên quan. Trong bài toán này, ta cần xác định các vectơ SA, SB, AB, BC.
Bước 2: Chọn hệ tọa độ. Ta chọn hệ tọa độ Oxyz với gốc O trùng với điểm A, trục Ox trùng với đường thẳng AB, trục Oy trùng với đường thẳng AD, trục Oz trùng với đường thẳng SA.
Bước 3: Biểu diễn các vectơ bằng tọa độ. Dựa vào hệ tọa độ đã chọn, ta có:
Từ đó, ta có:
Bước 4: Tính góc giữa đường thẳng SB và mặt phẳng (ABCD). Gọi φ là góc giữa đường thẳng SB và mặt phẳng (ABCD). Ta có:
sin φ = SA / SB = a / √(a² + a²) = 1 / √2
Suy ra φ = arcsin(1 / √2) = 45°
Vậy, góc giữa đường thẳng SB và mặt phẳng (ABCD) là 45°.
Để củng cố kiến thức về vectơ và ứng dụng trong không gian, các em có thể tham khảo các bài tập tương tự sau:
Ngoài ra, các em có thể tìm hiểu thêm về các ứng dụng của vectơ trong hình học không gian, vật lý và các lĩnh vực khác.
Bài 11 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ nắm vững kiến thức và tự tin hơn trong quá trình học tập.