Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 8, 9 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học toán online hiệu quả, đồng thời cung cấp nguồn tài liệu học tập chất lượng cao, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết: Xét dấu của các tam thức bậc hai sau: trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = 2{x^2} - 3x - 2\)
b) \(g\left( x \right) = - {x^2} + 2x - 3\)
Phương pháp giải:
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xác định nghiệm của \(f\left( x \right)\) (nếu có) \(x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\)
Bước 3: Xác định dấu của hệ số \(a\)
Bước 4: Xác định dấu của \(f\left( x \right)\)
Lời giải chi tiết:
a) \(f\left( x \right) = 2{x^2} - 3x - 2\) có \(\Delta = 25 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{1}{2};{x_2} = 2\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
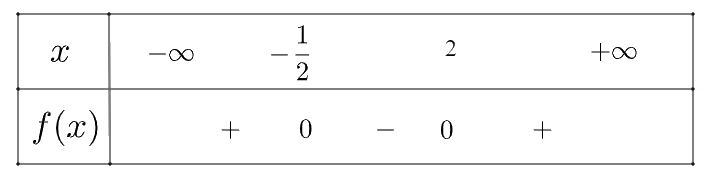
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \frac{1}{2},2} \right)\) và dương trong hai khoảng
\(\left( { - \infty , - \frac{1}{2}} \right)\) và \(\left( {2, + \infty } \right)\)
b) \(g\left( x \right) = - {x^2} + 2x - 3\) có \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 3} \right) = - 8 < 0\) và \(a = - 1 < 0\)
Vậy \(g\left( x \right)\)âm với mọi \(x \in \mathbb{R}\)
Xét dấu tam thức bậc hai \(h\left( x \right) = - 0,006{x^2} + 1,2x - 30\) trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu
Phương pháp giải:
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xác định nghiệm của \(h\left( x \right)\) (nếu có) \(x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\)
Bước 3: Xác định dấu của hệ số \(a\)
Bước 4: Xác định dấu của \(h\left( x \right)\)
Lời giải chi tiết:
\(h\left( x \right) = - 0,006{x^2} + 1,2x - 30\) có \(\Delta = 1,{2^2} - 4.\left( { - 0,006} \right).\left( { - 30} \right) = \frac{{18}}{{25}} > 0\), hai nghiệm phân biệt là \({x_1} = 100 - 50\sqrt 2 ;{x_2} = 100 + 50\sqrt 2 \) và \(a = - 0,006 < 0\)
Ta có bảng xét dấu \(h\left( x \right)\) như sau:
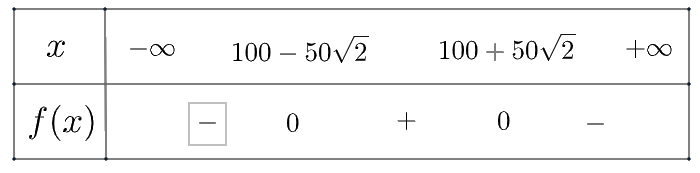
Vậy vòm cầu cao hơn mặt cầu là khoảng cách từ \(100 - 50\sqrt 2 \)(m) đến \(100 + 50\sqrt 2 \) (m) (cách từ O), vòm vòm cầu thấp hơn mặt cầu là khoảng cách từ O đến\(100 - 50\sqrt 2 \)(m) và từ \(100 + 50\sqrt 2 \) (m) đến 200 (m) (cách từ O)
Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết:
+) Các nghiệm (nếu có) và dấu của biệt thức \(\Delta \)
+) Các khoảng giá trị của \(x\)mà trên đó \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\)

Phương pháp giải:
Bước 1: Xác định nghiệm của hàm số là giao của đồ thị và trục hoành
Bước 2: Xác định biệt thức \(\Delta = {b^2} - 4ac\) và xác định dấu của nó
Bước 3: Dựa vào đồ thị xác định dấu của \(f\left( x \right)\)
+) Phần đồ thị nằm trên trục hoành là \(f\left( x \right) > 0\)
+) Phần đồ thị nằm dưới trục hoành là \(f\left( x \right) < 0\)
Lời giải chi tiết:
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
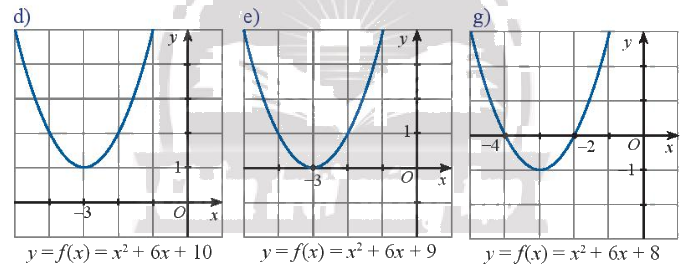
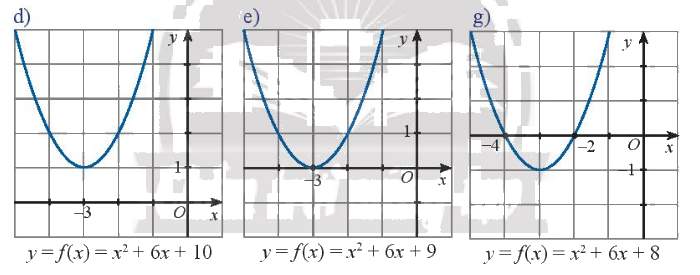
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết:
+) Các nghiệm (nếu có) và dấu của biệt thức \(\Delta \)
+) Các khoảng giá trị của \(x\)mà trên đó \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\)
Phương pháp giải:
Bước 1: Xác định nghiệm của hàm số là giao của đồ thị và trục hoành
Bước 2: Xác định biệt thức \(\Delta = {b^2} - 4ac\) và xác định dấu của nó
Bước 3: Dựa vào đồ thị xác định dấu của \(f\left( x \right)\)
+) Phần đồ thị nằm trên trục hoành là \(f\left( x \right) > 0\)
+) Phần đồ thị nằm dưới trục hoành là \(f\left( x \right) < 0\)
Lời giải chi tiết:
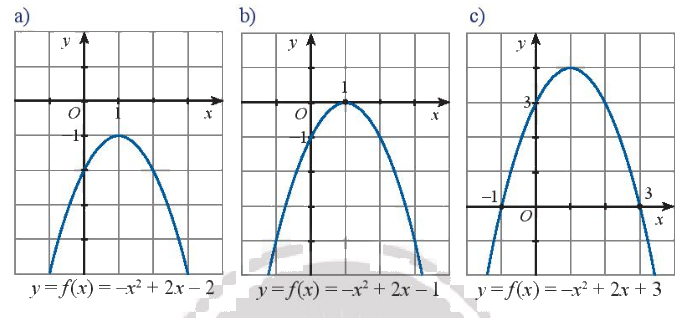
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = 2{x^2} - 3x - 2\)
b) \(g\left( x \right) = - {x^2} + 2x - 3\)
Phương pháp giải:
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xác định nghiệm của \(f\left( x \right)\) (nếu có) \(x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\)
Bước 3: Xác định dấu của hệ số \(a\)
Bước 4: Xác định dấu của \(f\left( x \right)\)
Lời giải chi tiết:
a) \(f\left( x \right) = 2{x^2} - 3x - 2\) có \(\Delta = 25 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{1}{2};{x_2} = 2\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
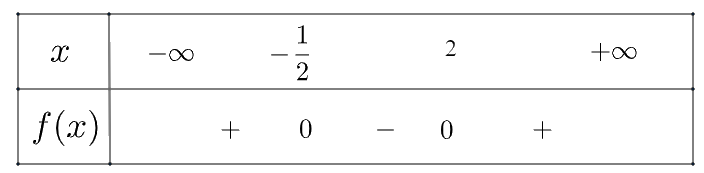
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \frac{1}{2},2} \right)\) và dương trong hai khoảng
\(\left( { - \infty , - \frac{1}{2}} \right)\) và \(\left( {2, + \infty } \right)\)
b) \(g\left( x \right) = - {x^2} + 2x - 3\) có \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 3} \right) = - 8 < 0\) và \(a = - 1 < 0\)
Vậy \(g\left( x \right)\)âm với mọi \(x \in \mathbb{R}\)
Xét dấu tam thức bậc hai \(h\left( x \right) = - 0,006{x^2} + 1,2x - 30\) trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu
Phương pháp giải:
Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xác định nghiệm của \(h\left( x \right)\) (nếu có) \(x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\)
Bước 3: Xác định dấu của hệ số \(a\)
Bước 4: Xác định dấu của \(h\left( x \right)\)
Lời giải chi tiết:
\(h\left( x \right) = - 0,006{x^2} + 1,2x - 30\) có \(\Delta = 1,{2^2} - 4.\left( { - 0,006} \right).\left( { - 30} \right) = \frac{{18}}{{25}} > 0\), hai nghiệm phân biệt là \({x_1} = 100 - 50\sqrt 2 ;{x_2} = 100 + 50\sqrt 2 \) và \(a = - 0,006 < 0\)
Ta có bảng xét dấu \(h\left( x \right)\) như sau:
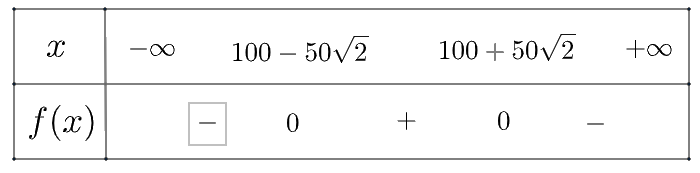
Vậy vòm cầu cao hơn mặt cầu là khoảng cách từ \(100 - 50\sqrt 2 \)(m) đến \(100 + 50\sqrt 2 \) (m) (cách từ O), vòm vòm cầu thấp hơn mặt cầu là khoảng cách từ O đến\(100 - 50\sqrt 2 \)(m) và từ \(100 + 50\sqrt 2 \) (m) đến 200 (m) (cách từ O)
Mục 2 trong SGK Toán 10 tập 2 chương trình Chân trời sáng tạo tập trung vào việc ôn tập chương 1 và giới thiệu một số khái niệm cơ bản về hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng kiến thức về tập hợp, số thực, bất phương trình và hàm số để giải quyết các vấn đề thực tế.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận về các khái niệm cơ bản của tập hợp, số thực, bất phương trình và hàm số. Để giải quyết bài tập này, học sinh cần nắm vững định nghĩa, tính chất và các quy tắc cơ bản của các khái niệm này.
Bài 2 giới thiệu về hàm số bậc hai y = ax² + bx + c, với a ≠ 0. Học sinh cần hiểu rõ các khái niệm về parabol, đỉnh của parabol, trục đối xứng và giao điểm của parabol với các trục tọa độ.
Để giải các bài tập trong mục 2 trang 8, 9 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Tìm tọa độ đỉnh của parabol y = x² - 4x + 3.
Giải:
Hàm số y = x² - 4x + 3 có dạng y = ax² + bx + c, với a = 1, b = -4 và c = 3.
Tọa độ đỉnh của parabol là (x₀, y₀), với x₀ = -b/2a = -(-4)/(2*1) = 2 và y₀ = f(x₀) = f(2) = 2² - 4*2 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2, -1).
Khi giải các bài tập về hàm số bậc hai, học sinh cần chú ý đến điều kiện xác định của hàm số và các trường hợp đặc biệt. Ngoài ra, việc vẽ đồ thị của hàm số cũng giúp học sinh hiểu rõ hơn về tính chất của hàm số và tìm ra lời giải chính xác.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập trong mục 2 trang 8, 9 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tốt!
| Khái niệm | Định nghĩa |
|---|---|
| Hàm số bậc hai | Hàm số có dạng y = ax² + bx + c, với a ≠ 0 |
| Parabol | Đồ thị của hàm số bậc hai |
| Đỉnh của parabol | Điểm thấp nhất (hoặc cao nhất) trên parabol |