Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 67, 68, 69 sách giáo khoa Toán 10 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
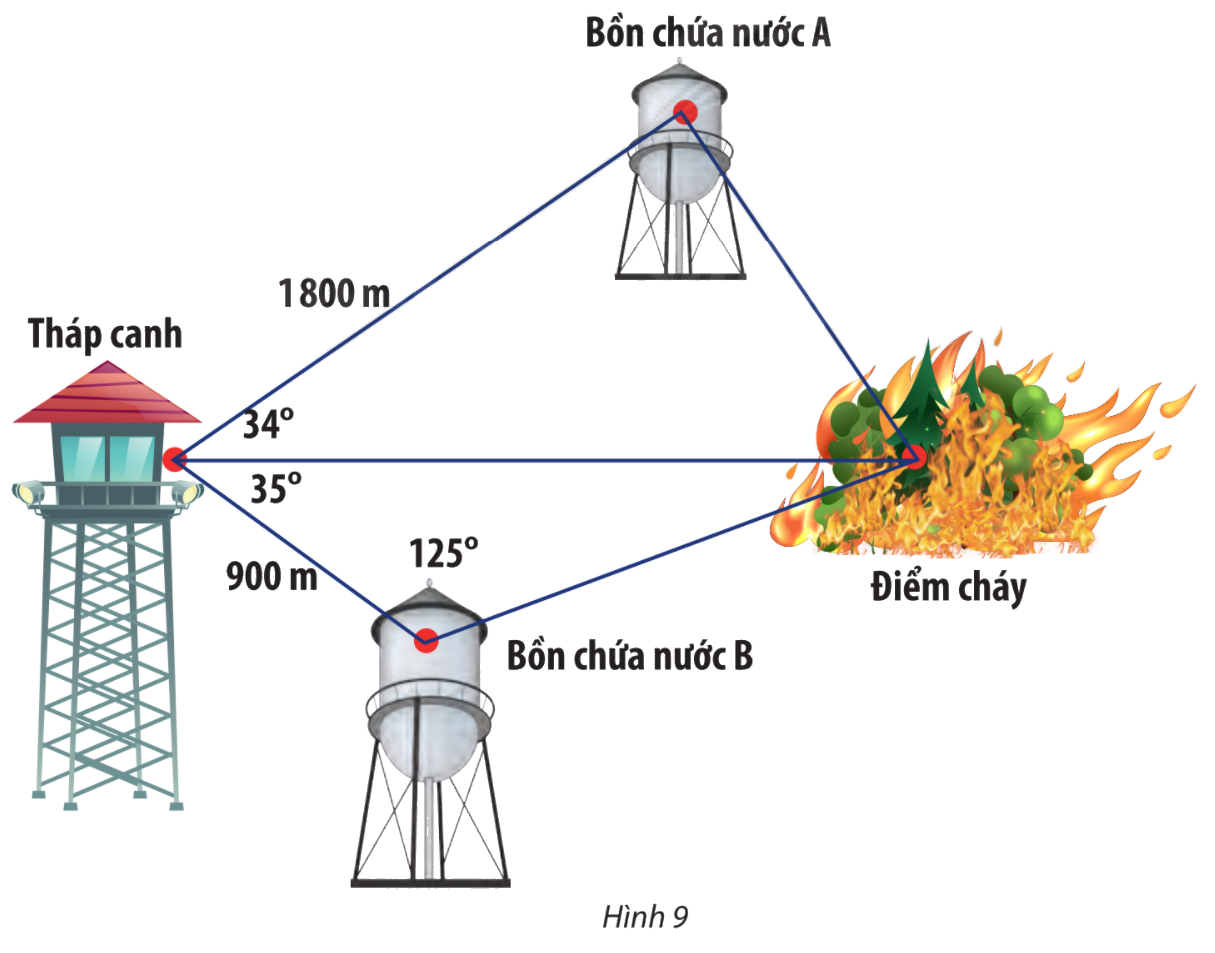
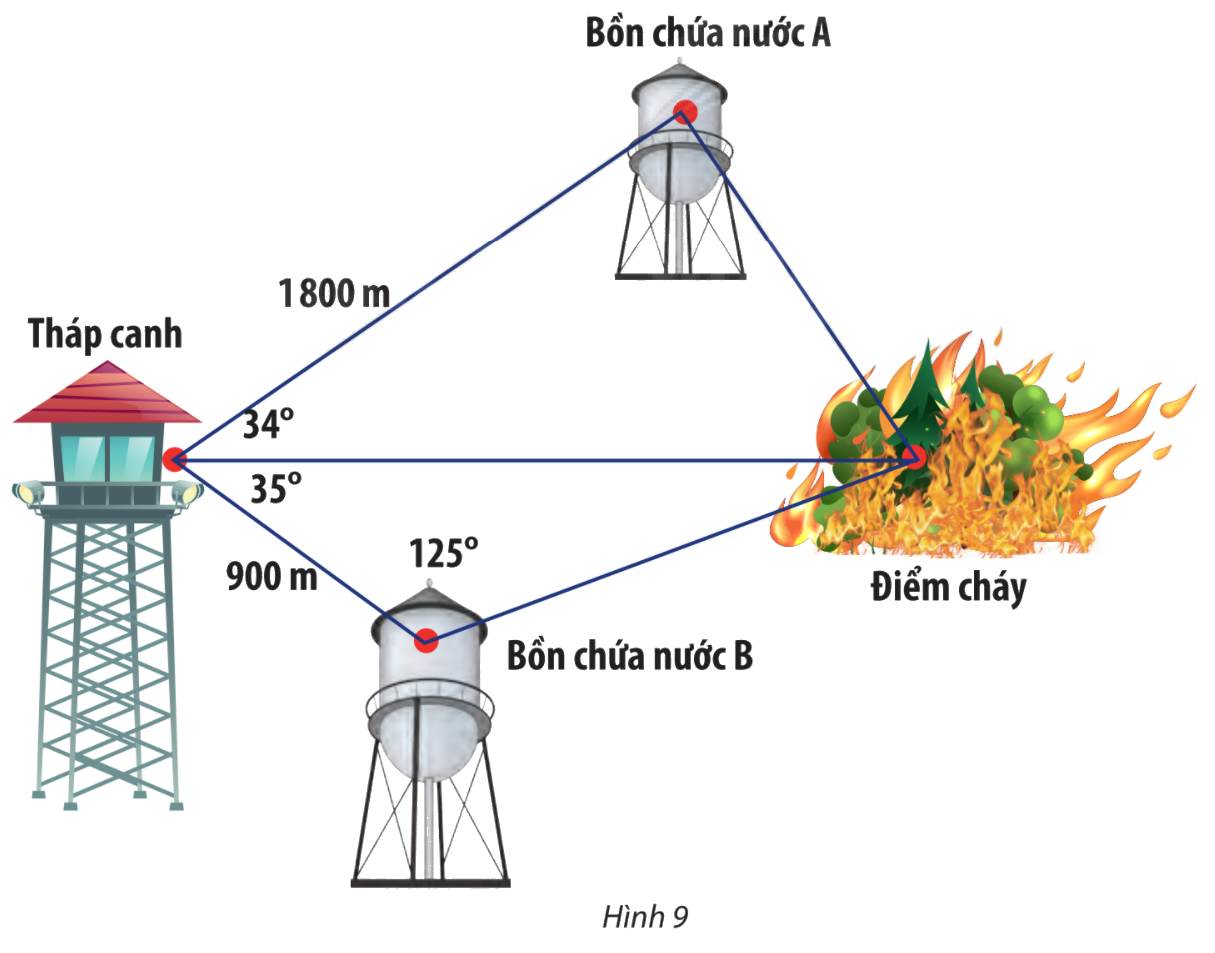
Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?
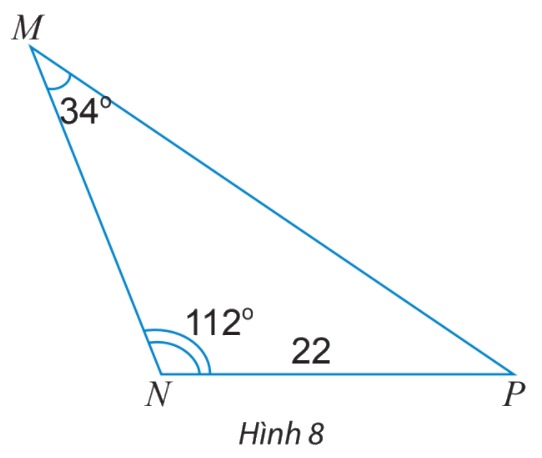
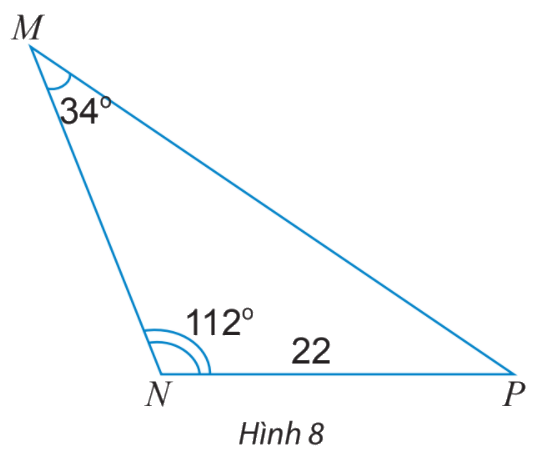
Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
Phương pháp giải:
Áp dụng định lí sin cho tam giác MNP:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)
Lời giải chi tiết:
Ta có: \(NP = 22,\;\widehat P = {180^o} - ({112^o} + {34^o}) = {34^o}\)
Áp dụng định lí sin, ta có:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)
Suy ra:
\(MP = \frac{{NP.\sin N}}{{\sin M}} = \frac{{22.\sin {{112}^o}}}{{\sin {{34}^o}}} \approx 36,48\)
\(MN = \frac{{NP.\sin P}}{{\sin M}} = \frac{{22.\sin {{34}^o}}}{{\sin {{34}^o}}} = 22.\)
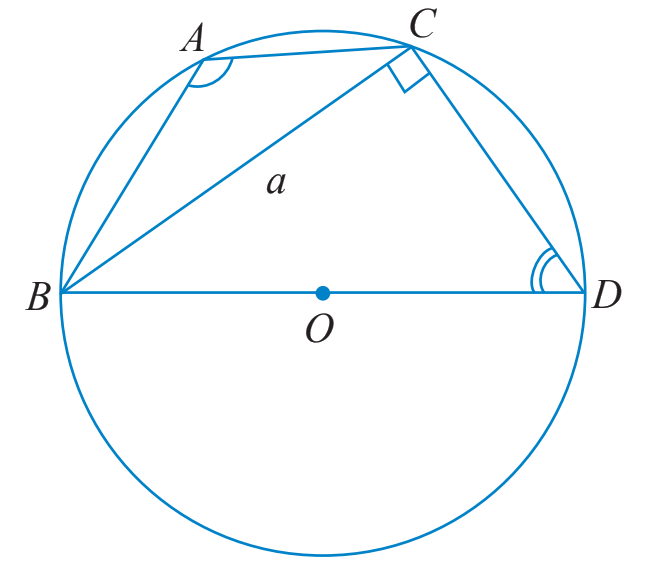
a) Cho tam giác ABC không phải là tam giác vuông có \(BC = a,AC = b,AB = c\) và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính \(\sin \widehat {BDC}\) theo a và R.
ii) Tìm mối liên hệ giữa hai góc \(\widehat {BAC}\) và \(\widehat {BDC}\). Từ đó chứng minh rằng \(2R = \frac{a}{{\sin A}}.\)
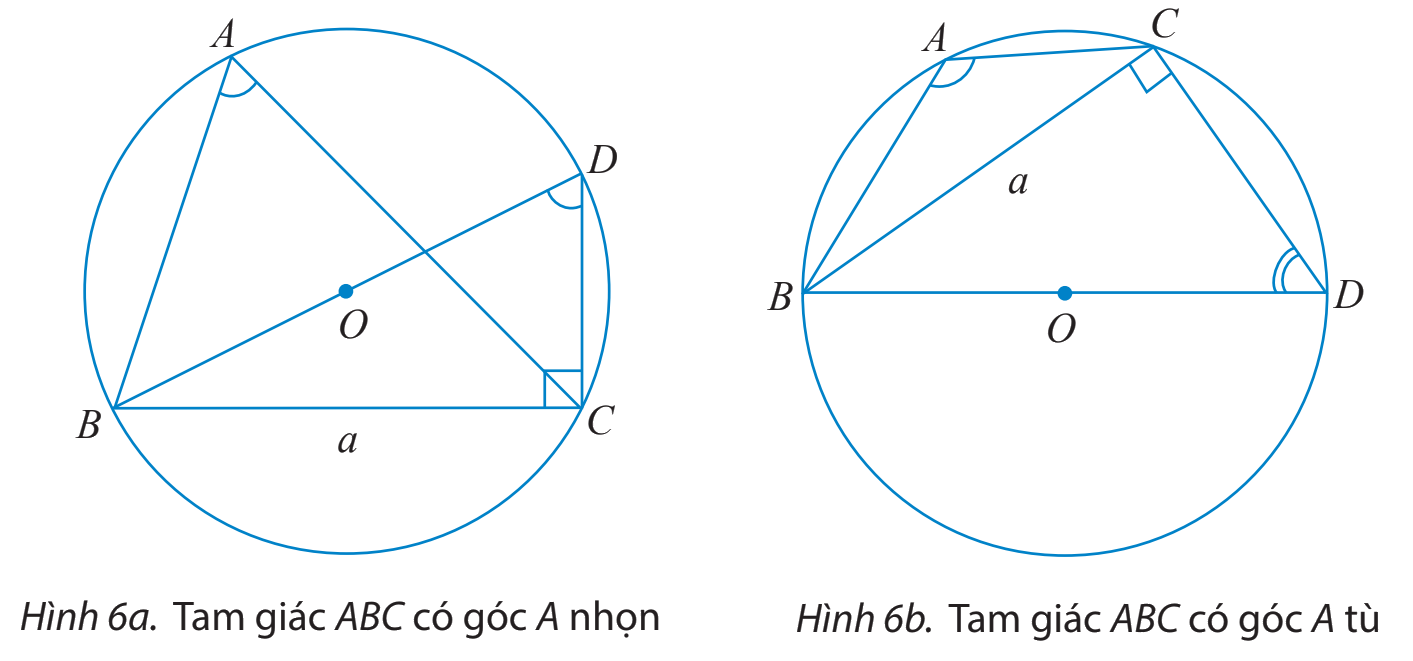
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức \(2R = \frac{a}{{\sin A}}.\)
Lời giải chi tiết:
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
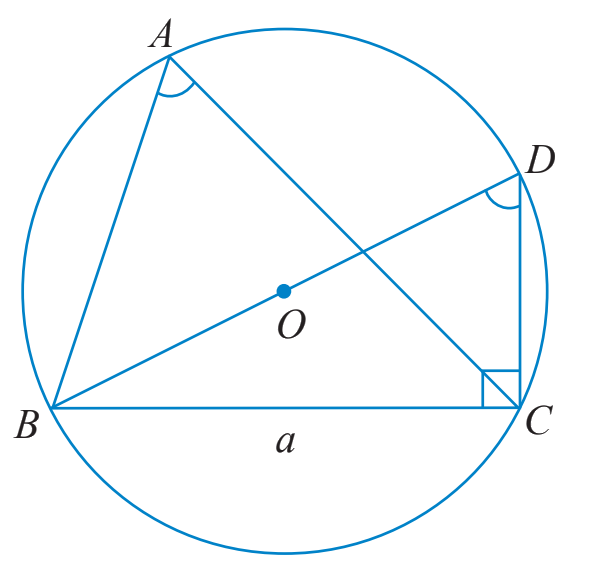
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
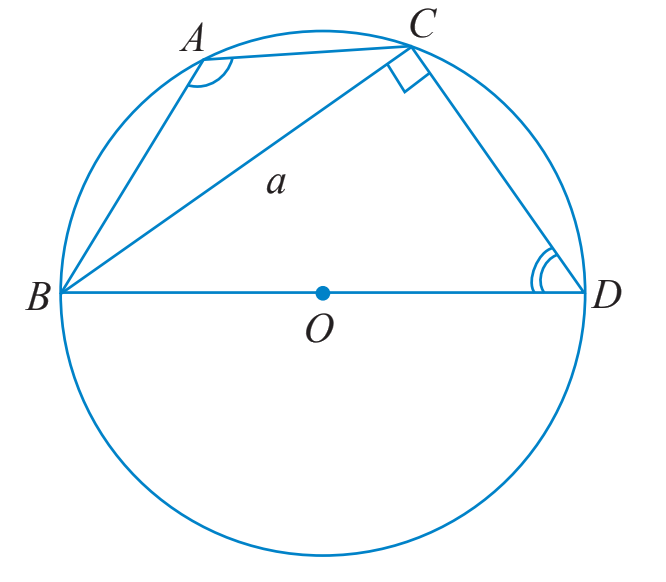
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)
Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?
Phương pháp giải:
Áp dụng định lí sin, tính khoảng cách từ bồn chứa nước A đến đám cháy.
Áp dụng định lí cosin, tính khoảng cách từ bồn chứa nước B đến đám cháy.
Lời giải chi tiết:
Đặt các điểm A, B, C, D lần lượt là vị trí bồn chứa nước A, bồn chứa nước B, tháp canh và đám cháy.
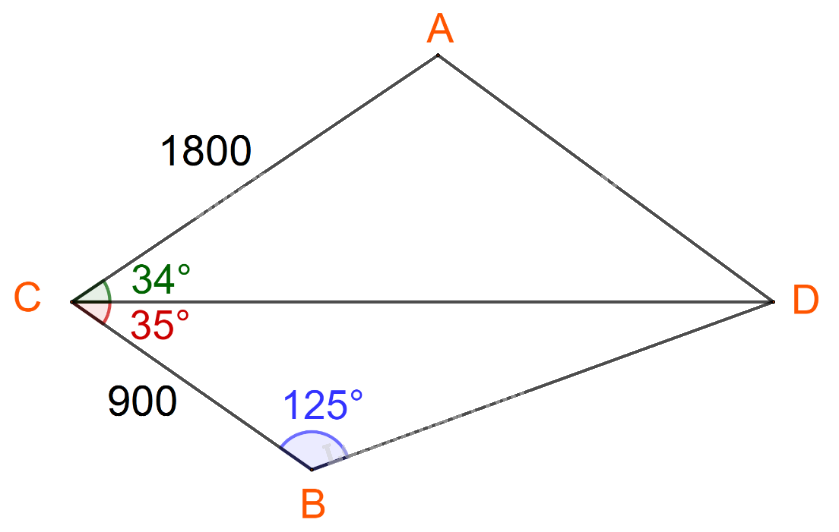
Ta có: \(CB = 900,\;\widehat {CDB} = {180^o} - ({125^o} + {35^o}) = {20^o}\)
Áp dụng định lí sin trong tam giác CBD, ta có:
\(\frac{{CB}}{{\sin D}} = \frac{{BD}}{{\sin C}} = \frac{{CD}}{{\sin B}}\)
Suy ra:
\(BD = \frac{{CB.\sin C}}{{\sin D}} = \frac{{900.\sin {{35}^o}}}{{\sin {{20}^o}}} \approx 1509,3\)
\(CD = \frac{{CB.\sin B}}{{\sin D}} = \frac{{900.\sin {{125}^o}}}{{\sin {{20}^o}}} = 2155,5\)
Áp dụng định lí cosin trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = A{C^2} + C{D^2} - 2.AC.CD.\cos \widehat {ACD}\\ \Leftrightarrow A{D^2} = {1800^2} + 2155,{5^2} - 2.1800.2155,5.\cos {34^o} \approx 1453014,5\\ \Leftrightarrow AD \approx 1205,4\end{array}\)
Vì \(AD < BD\) nên khoảng cách từ bồn chứa nước A đến đám cháy là ngắn hơn.
Vậy nên dẫn nước từ bồn chứa nước A để dập tắt đám cháy nhanh hơn.
a) Cho tam giác ABC không phải là tam giác vuông có \(BC = a,AC = b,AB = c\) và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính \(\sin \widehat {BDC}\) theo a và R.
ii) Tìm mối liên hệ giữa hai góc \(\widehat {BAC}\) và \(\widehat {BDC}\). Từ đó chứng minh rằng \(2R = \frac{a}{{\sin A}}.\)
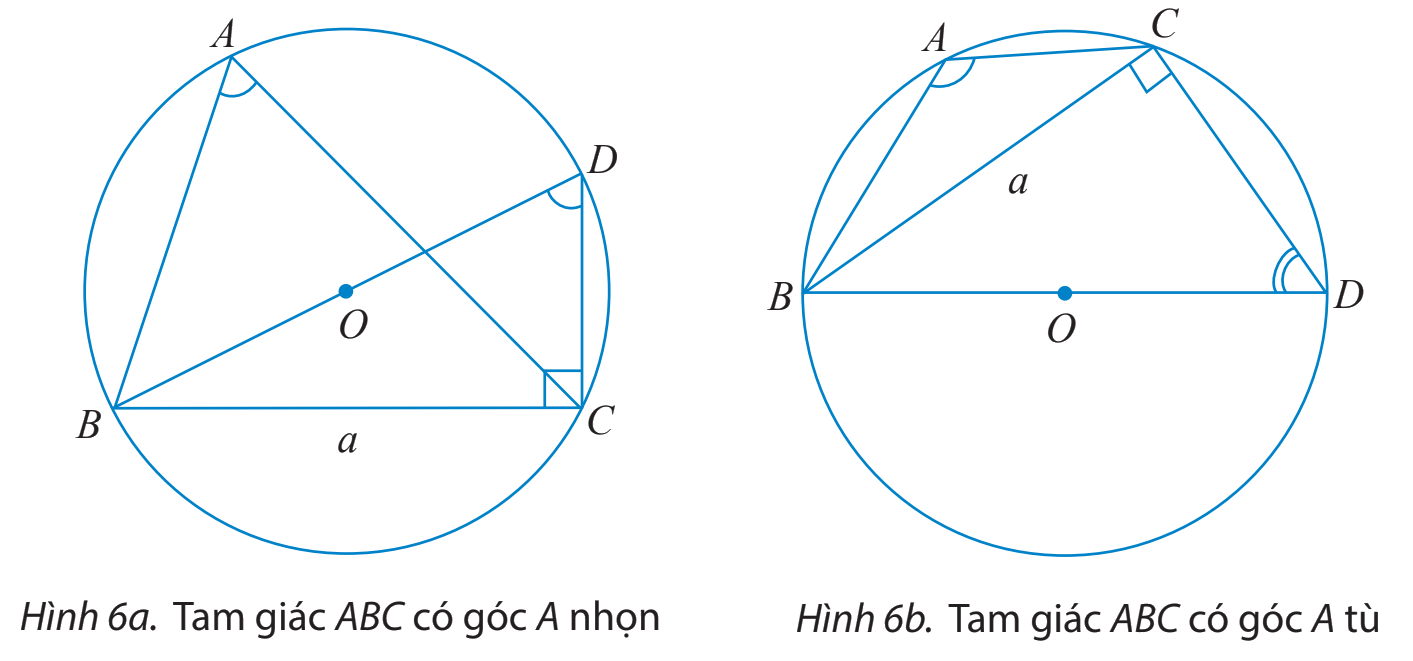
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức \(2R = \frac{a}{{\sin A}}.\)
Lời giải chi tiết:
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
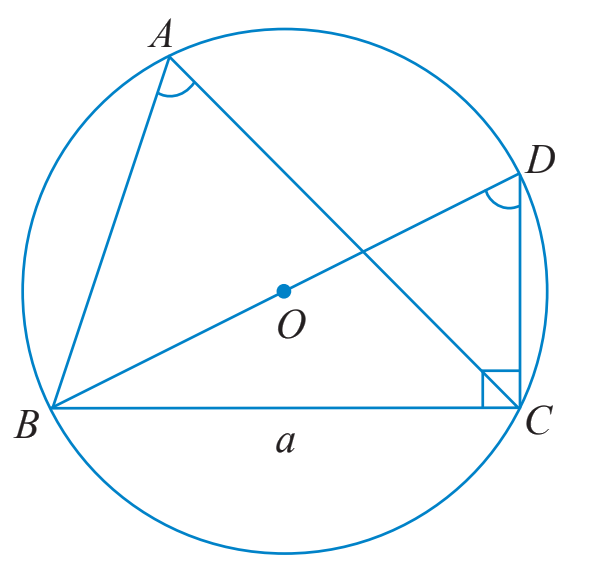
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)
Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
Phương pháp giải:
Áp dụng định lí sin cho tam giác MNP:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)
Lời giải chi tiết:
Ta có: \(NP = 22,\;\widehat P = {180^o} - ({112^o} + {34^o}) = {34^o}\)
Áp dụng định lí sin, ta có:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)
Suy ra:
\(MP = \frac{{NP.\sin N}}{{\sin M}} = \frac{{22.\sin {{112}^o}}}{{\sin {{34}^o}}} \approx 36,48\)
\(MN = \frac{{NP.\sin P}}{{\sin M}} = \frac{{22.\sin {{34}^o}}}{{\sin {{34}^o}}} = 22.\)
Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?
Phương pháp giải:
Áp dụng định lí sin, tính khoảng cách từ bồn chứa nước A đến đám cháy.
Áp dụng định lí cosin, tính khoảng cách từ bồn chứa nước B đến đám cháy.
Lời giải chi tiết:
Đặt các điểm A, B, C, D lần lượt là vị trí bồn chứa nước A, bồn chứa nước B, tháp canh và đám cháy.
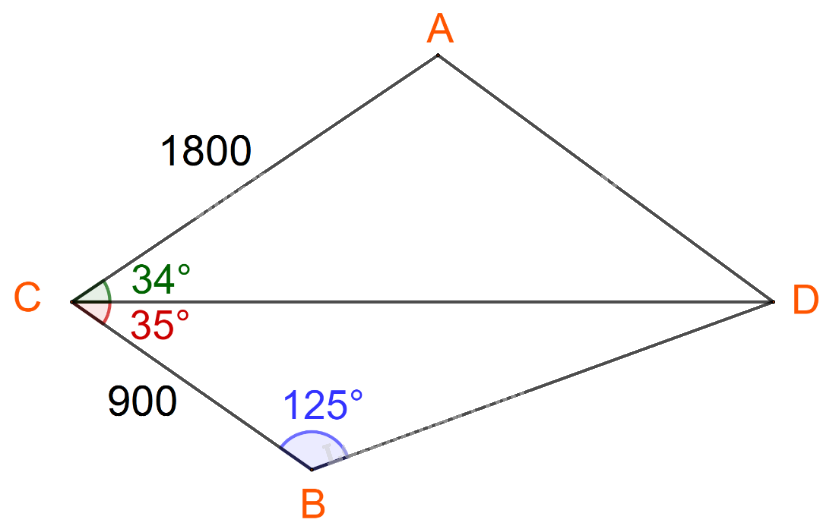
Ta có: \(CB = 900,\;\widehat {CDB} = {180^o} - ({125^o} + {35^o}) = {20^o}\)
Áp dụng định lí sin trong tam giác CBD, ta có:
\(\frac{{CB}}{{\sin D}} = \frac{{BD}}{{\sin C}} = \frac{{CD}}{{\sin B}}\)
Suy ra:
\(BD = \frac{{CB.\sin C}}{{\sin D}} = \frac{{900.\sin {{35}^o}}}{{\sin {{20}^o}}} \approx 1509,3\)
\(CD = \frac{{CB.\sin B}}{{\sin D}} = \frac{{900.\sin {{125}^o}}}{{\sin {{20}^o}}} = 2155,5\)
Áp dụng định lí cosin trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = A{C^2} + C{D^2} - 2.AC.CD.\cos \widehat {ACD}\\ \Leftrightarrow A{D^2} = {1800^2} + 2155,{5^2} - 2.1800.2155,5.\cos {34^o} \approx 1453014,5\\ \Leftrightarrow AD \approx 1205,4\end{array}\)
Vì \(AD < BD\) nên khoảng cách từ bồn chứa nước A đến đám cháy là ngắn hơn.
Vậy nên dẫn nước từ bồn chứa nước A để dập tắt đám cháy nhanh hơn.
Mục 2 của SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức cơ bản về tập hợp số, bao gồm số thực, các phép toán trên số thực, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về cộng, trừ, nhân, chia số thực để thực hiện các phép tính đơn giản. Các em cần lưu ý thứ tự thực hiện các phép toán và các quy tắc dấu.
Bài tập này tập trung vào việc kiểm tra sự hiểu biết của học sinh về các tính chất giao hoán, kết hợp, phân phối của các phép toán trên số thực. Việc nắm vững các tính chất này giúp học sinh giải toán nhanh chóng và chính xác hơn.
Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải các bài toán thực tế. Các bài toán này thường liên quan đến việc tính toán diện tích, chu vi, thể tích, hoặc các đại lượng vật lý khác.
| Bài tập | Hướng dẫn |
|---|---|
| Tính diện tích của một hình chữ nhật có chiều dài 5cm và chiều rộng 3cm. | Diện tích = chiều dài * chiều rộng = 5cm * 3cm = 15cm2 |
Để giải bài tập trong mục 2 trang 67, 68, 69 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo một cách hiệu quả, các em cần:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 67, 68, 69 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!