Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 21, 22, 23 sách giáo khoa Toán 10 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):
Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x - y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x - y = 1\} \)
Hãy xác định \(A \cap B\).
Phương pháp giải:
\(A \cap B = \{ (x;y)|(x;y) \in A\) và \((x;y) \in B\} \)
Lời giải chi tiết:
a) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},3x - y = 9,x - y = 1\} \)
Tức là \(A \cap B\)là tập hợp các cặp số (x;y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 9\\x - y = 1\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y = 3x - 9\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 3x - 9\\y = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 8\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\end{array}\)
Vậy \(A \cap B = \{ (4;3)\} .\)
Xác định các tập hợp \(A \cup B\) và \(A \cap B\), biết:
a) \(A = \{ a;b;c;d;e\} \), \(B = \{ a;e;i;u\} \)
b) \(A = \{ x \in \mathbb{R}|\;{x^2} + 2x - 3 = 0\} \),\(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \)
Phương pháp giải:
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
Lời giải chi tiết:
a) \(A \cup B = \{ a;b;c;d;e;i;u\} \), \(A \cap B = \{ a;e\} \)
b) Phương trình \({x^2} + 2x - 3 = 0\) có hai nghiệm là 1 và -3, nên \(A = \{ 1; - 3\} \)
Phương trình \(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \) có hai nghiệm là 1 và -1, nên \(B = \{ 1; - 1\} \)
Từ đó, \(A \cup B = \{ 1; - 1; - 3\} \), \(A \cap B = \{ 1\} .\)
Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?
Phương pháp giải:
Kí hiệu A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.
Sử dụng biểu đồ Ven, minh họa tập hợp các khán giả đã tham gia bình chọn (\(A \cup B\)) và các khán giả không tham gia bình chọn.
Lời giải chi tiết:
Gọi A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.
Theo giả thiết, \(n(A) = 85,n(B) = 72,n(A \cap B) = 60\)
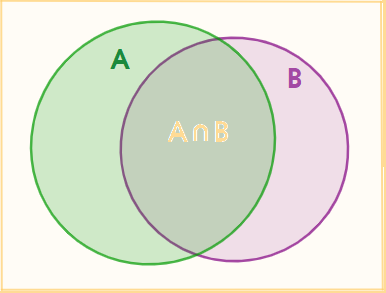
Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số khán giả đã tham gia bình chọn, nhưng số khán giả bình chọn cho cả hai thí sinh được tính hai lần. Do đó, số khán giả đã tham gia bình chọn là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 85 + 72 - 60 = 97\)
Như vậy trong hội trường 100 khán giả, có 97 khán giải đã tham gia bình chọn, còn lại số khán giả không tham gia bình chọn là: \(100 - 97 = 3\) (khán giả).
Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm
65 | 75 | 78 | 82 | 90 | |||
94 | 100 | 120 | 231 | ||||
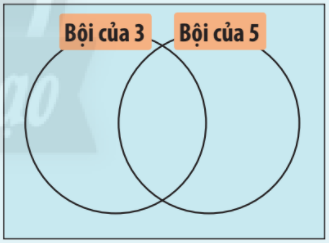
Phương pháp giải:
Phân biệt các miền trong hình chữ nhật
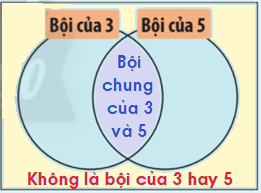
Lời giải chi tiết:
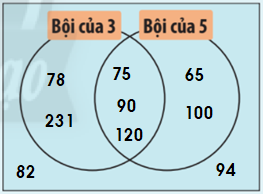
Bội của 3: 75, 78, 90, 120, 231
Bội của 5: 65, 75, 90, 100, 120
Vừa là bội của 3, vừa là bội của 5: 75, 90, 120.
Không là bội của 3 và không là bội của 5: 82, 94
Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):

a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.
c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

Lời giải chi tiết:
a) Tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn là:
\(A = \{ {a_1};{a_2};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)
Tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ là:
\(B = \{ {a_1};{a_3};{a_5};{a_6};{a_8};{a_{10}}\} \)
b) Tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ là:
\(C = \{ {a_1};{a_5};{a_6};{a_8};{a_{10}}\} \)
c) Tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ là:
\(D = \{ {a_1};{a_2};{a_3};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)
Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm
65 | 75 | 78 | 82 | 90 | |||
94 | 100 | 120 | 231 | ||||
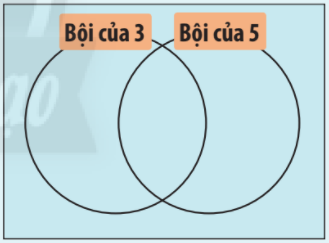
Phương pháp giải:
Phân biệt các miền trong hình chữ nhật
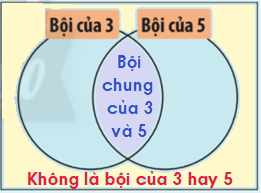
Lời giải chi tiết:
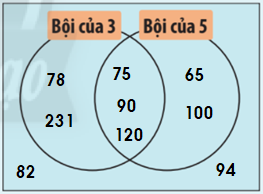
Bội của 3: 75, 78, 90, 120, 231
Bội của 5: 65, 75, 90, 100, 120
Vừa là bội của 3, vừa là bội của 5: 75, 90, 120.
Không là bội của 3 và không là bội của 5: 82, 94
Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):

a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.
c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

Lời giải chi tiết:
a) Tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn là:
\(A = \{ {a_1};{a_2};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)
Tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ là:
\(B = \{ {a_1};{a_3};{a_5};{a_6};{a_8};{a_{10}}\} \)
b) Tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ là:
\(C = \{ {a_1};{a_5};{a_6};{a_8};{a_{10}}\} \)
c) Tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ là:
\(D = \{ {a_1};{a_2};{a_3};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)
Xác định các tập hợp \(A \cup B\) và \(A \cap B\), biết:
a) \(A = \{ a;b;c;d;e\} \), \(B = \{ a;e;i;u\} \)
b) \(A = \{ x \in \mathbb{R}|\;{x^2} + 2x - 3 = 0\} \),\(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \)
Phương pháp giải:
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
Lời giải chi tiết:
a) \(A \cup B = \{ a;b;c;d;e;i;u\} \), \(A \cap B = \{ a;e\} \)
b) Phương trình \({x^2} + 2x - 3 = 0\) có hai nghiệm là 1 và -3, nên \(A = \{ 1; - 3\} \)
Phương trình \(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \) có hai nghiệm là 1 và -1, nên \(B = \{ 1; - 1\} \)
Từ đó, \(A \cup B = \{ 1; - 1; - 3\} \), \(A \cap B = \{ 1\} .\)
Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x - y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x - y = 1\} \)
Hãy xác định \(A \cap B\).
Phương pháp giải:
\(A \cap B = \{ (x;y)|(x;y) \in A\) và \((x;y) \in B\} \)
Lời giải chi tiết:
a) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},3x - y = 9,x - y = 1\} \)
Tức là \(A \cap B\)là tập hợp các cặp số (x;y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 9\\x - y = 1\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y = 3x - 9\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 3x - 9\\y = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 8\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\end{array}\)
Vậy \(A \cap B = \{ (4;3)\} .\)
Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?
Phương pháp giải:
Kí hiệu A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.
Sử dụng biểu đồ Ven, minh họa tập hợp các khán giả đã tham gia bình chọn (\(A \cup B\)) và các khán giả không tham gia bình chọn.
Lời giải chi tiết:
Gọi A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.
Theo giả thiết, \(n(A) = 85,n(B) = 72,n(A \cap B) = 60\)
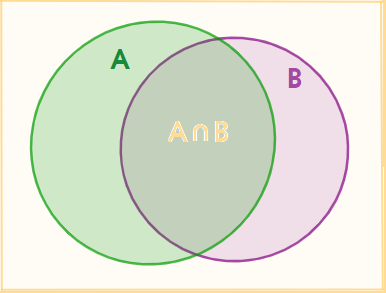
Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số khán giả đã tham gia bình chọn, nhưng số khán giả bình chọn cho cả hai thí sinh được tính hai lần. Do đó, số khán giả đã tham gia bình chọn là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 85 + 72 - 60 = 97\)
Như vậy trong hội trường 100 khán giả, có 97 khán giải đã tham gia bình chọn, còn lại số khán giả không tham gia bình chọn là: \(100 - 97 = 3\) (khán giả).
Mục 1 của chương trình Toán 10 tập 1 - Chân trời sáng tạo tập trung vào việc giới thiệu các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Đây là nền tảng quan trọng để học sinh có thể tiếp cận các kiến thức phức tạp hơn trong các chương tiếp theo.
Bài tập này yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán hợp, giao, hiệu, bù của các tập hợp, và chứng minh các tính chất liên quan. Để giải quyết các bài tập này, học sinh cần nắm vững định nghĩa và các quy tắc cơ bản về tập hợp.
Bài tập này tập trung vào việc chứng minh các tính chất của phép hợp, giao, hiệu, bù của các tập hợp, như tính giao hoán, tính kết hợp, tính phân phối. Để giải quyết các bài tập này, học sinh cần sử dụng các định nghĩa và các quy tắc logic.
Bài tập này yêu cầu học sinh sử dụng kiến thức về tập hợp để giải quyết các bài toán thực tế, như bài toán đếm, bài toán tìm tập hợp thỏa mãn các điều kiện cho trước. Để giải quyết các bài tập này, học sinh cần kết hợp kiến thức về tập hợp với các kiến thức khác trong chương trình Toán học.
| Tập hợp A | Tập hợp B | A ∪ B |
|---|---|---|
| {1, 2, 3} | {4, 5, 6} | {1, 2, 3, 4, 5, 6} |
Để giải quyết hiệu quả các bài tập về tập hợp, học sinh nên:
Hy vọng rằng với lời giải chi tiết và các lời khuyên trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về tập hợp trong SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!