Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về Khái niệm Vectơ, một trong những kiến thức cơ bản và quan trọng trong chương trình Toán học.
Chúng tôi sẽ trình bày các định nghĩa, tính chất, và các phép toán liên quan đến Vectơ một cách dễ hiểu, giúp bạn nắm vững kiến thức và áp dụng vào giải bài tập một cách hiệu quả.
1. ĐỊNH NGHĨA VECTƠ
1. ĐỊNH NGHĨA VECTƠ
+) Vecto là một đoạn thẳng có hướng.
Ví dụ: i) vecto \(\overrightarrow {AB} \): (đọc là vecto AB)

ii) Vecto \(\overrightarrow {BA} \):

iii) vecto \(\overrightarrow u \): (khi không chỉ rõ điểm đầu, điểm cuối)
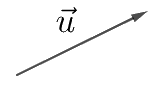
+) Giá của vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.
Ví dụ: Giá của vecto \(\overrightarrow {CD} \) là đường thẳng CD
+) Độ dài của vecto là \(\overrightarrow {AB} \) là độ dài đoạn thẳng AB.
Kí hiệu: \(\left| {\overrightarrow {AB} } \right|\) và \(\left| {\overrightarrow {AB} } \right| = AB\).
2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.
Ví dụ:
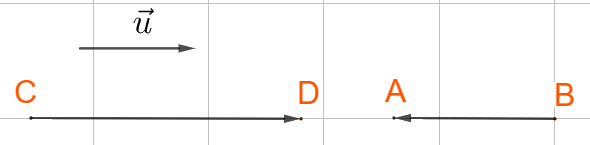
Ba vecto \(\overrightarrow u ,\;\overrightarrow {CD} ,\;\overrightarrow {AB} \) cùng phương.
Trong đó 2 vecto \(\overrightarrow u ,\;\overrightarrow {CD} \) cùng hướng, còn 2 vecto \(\overrightarrow {CD} ,\;\overrightarrow {AB} \) ngược hướng.
+) Ba điểm A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
3. HAI VECTƠ BẰNG NHAU - VECTƠ ĐỐI NHAU
+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
+) Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng.
Kí hiệu: \(\overrightarrow a = - \overrightarrow b \) (vecto \(\overrightarrow b \) là vecto đối của vecto \(\overrightarrow a \))
+) Với mỗi điểm O và vecto \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \)
4. VECTƠ - KHÔNG
+) Vecto không, là vecto có điểm đầu và điểm cuối trùng nhau. Ví dụ: \(\overrightarrow {AA} ,\;\overrightarrow {EE} ,...\)
Kí hiệu chung là \(\overrightarrow 0 \).
* Chú ý:
- Vecto không có độ dài bằng 0.
- Vecto \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vecto.
- Mọi vecto-không đều bằng nhau: \(\overrightarrow 0 = \overrightarrow {AA} = \;\overrightarrow {BB} = ...\)
- Vecto đối của vecto-không là chính nó.
Vectơ là một khái niệm cơ bản và quan trọng trong toán học, đặc biệt trong hình học và vật lý. Nó được sử dụng để biểu diễn cả độ lớn và hướng của một đại lượng. Bài viết này sẽ trình bày chi tiết về khái niệm vectơ, các loại vectơ, các phép toán trên vectơ và ứng dụng của vectơ trong giải toán.
Một vectơ là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Vectơ thường được ký hiệu bằng một chữ cái in hoa hoặc một cặp điểm, ví dụ: AB hoặc a.
Có nhiều loại vectơ khác nhau, bao gồm:
Có một số phép toán cơ bản trên vectơ, bao gồm:
Trong hệ tọa độ, một vectơ có thể được biểu diễn bằng các thành phần của nó. Ví dụ, trong hệ tọa độ Descartes hai chiều, một vectơ a có thể được biểu diễn bằng a = (x, y), trong đó x và y là các thành phần của vectơ.
Vectơ có nhiều ứng dụng trong toán học, vật lý và các lĩnh vực khác, bao gồm:
Ví dụ 1: Cho hai vectơ a = (1, 2) và b = (3, 4). Tính tổng của hai vectơ này.
Giải:a + b = (1 + 3, 2 + 4) = (4, 6)
Ví dụ 2: Cho vectơ a = (2, -1) và số thực k = 3. Tính tích của vectơ a với số thực k.
Giải:k * a = (3 * 2, 3 * -1) = (6, -3)
Lý thuyết Khái niệm Vectơ là nền tảng quan trọng để hiểu và giải quyết các bài toán trong toán học và các lĩnh vực liên quan. Việc nắm vững các định nghĩa, tính chất và phép toán trên vectơ sẽ giúp bạn tự tin hơn trong việc học tập và làm việc.