Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 81 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ bạn giải quyết mọi khó khăn trong môn Toán.
Hai chiếc tàu thủy P và Q cách nhau 50 m.
Đề bài
Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = 40^\circ \) và \(\widehat {BQA} = 52^\circ \). Tính chiều cao của tháp hải đăng đó.
Lời giải chi tiết
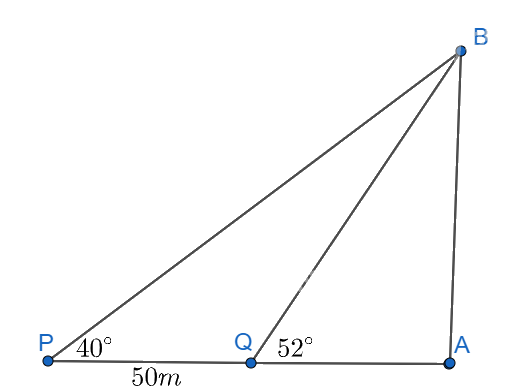
Góc \(\widehat {PQB}\) là góc bù của tam giác BPQ nên ta có:
\(\widehat {BQP} = \widehat {QPB} + \widehat {PBQ} \Rightarrow \widehat {PBQ} = \widehat {BQP} - \widehat {QPB} = 52^\circ - 40^\circ = 12^\circ \)
Áp dụng định lí sin trong tam giác BPQ ta có
\(\frac{{PQ}}{{\sin B}} = \frac{{BQ}}{{\sin P}} = \frac{{50}}{{\sin 12^\circ }} \Rightarrow BQ = \frac{{50}}{{\sin 12^\circ }}.\sin P = \frac{{50}}{{\sin 12^\circ }}.\sin 40^\circ \)
Áp dụng định lí sin vào tam giác ABQ ta có:
\(\frac{{BQ}}{{\sin A}} = \frac{{AB}}{{\sin Q}} \Rightarrow AB = \frac{{BQ}}{{\sin A}}.\sin Q = \frac{{\frac{{50}}{{\sin 12^\circ }}.\sin 40^\circ }}{{\sin 90^\circ }}.\sin 52^\circ \simeq 121,81\) (m)
Vậy chiều cao của tháp hải đăng là khoảng 121,81 m
Bài 3 trang 81 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 3 thường bao gồm các dạng bài tập sau:
Để tính tổng hai vectơ \vec{a}" và \vec{b}", ta thực hiện phép cộng theo tọa độ: \vec{a} + \vec{b} = (x_a + x_b, y_a + y_b)". Ví dụ, nếu \vec{a} = (1, 2)" và \vec{b} = (3, -1)" thì \vec{a} + \vec{b} = (1+3, 2-1) = (4, 1)".
Để tính hiệu hai vectơ \vec{a}" và \vec{b}", ta thực hiện phép trừ theo tọa độ: \vec{a} - \vec{b} = (x_a - x_b, y_a - y_b)". Ví dụ, nếu \vec{a} = (1, 2)" và \vec{b} = (3, -1)" thì \vec{a} - \vec{b} = (1-3, 2-(-1)) = (-2, 3)".
Để tính tích của một số k" với vectơ \vec{a}", ta nhân số k" với mỗi tọa độ của vectơ \vec{a}": k\vec{a} = (kx_a, ky_a)". Ví dụ, nếu \vec{a} = (1, 2)" và k = 3" thì 3\vec{a} = (3*1, 3*2) = (3, 6)".
Ví dụ: Cho \vec{a} = (2, -3)" và \vec{b} = (-1, 4)". Tính 2\vec{a} - \vec{b}".
Giải:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 10 Chân trời sáng tạo hoặc các nguồn tài liệu học tập khác.
Bài 3 trang 81 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng các kiến thức về vectơ vào giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.