Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách Giải bài 4 trang 76 sách bài tập Toán 10 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để giúp bạn hiểu rõ bản chất của bài toán.
Thang leo gợn song cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100 m và khoảng cách giữa hai chân là 240 cm
Đề bài
Thang leo gợn song cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100 m và khoảng cách giữa hai chân là 240 cm
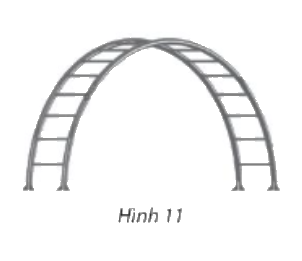
a) Hãy chọn hệ tọa độ thích hợp và viết phương trình chính tắc của elip nói trên
b) Tính khoảng cách thẳng đứng từ một điểm cách chân khủng 20 cm lên đến khung thép
Phương pháp giải - Xem chi tiết
Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} - {b^2}} \)
Lời giải chi tiết
a) Gọi phương trình chính tắc của elip là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
nửa hình elip cao 100 cm \( \Rightarrow b = 100\)
Khoảng cách giữa hai chân là 240 cm \( \Rightarrow 2a = 240 \Leftrightarrow a = 120\)
Vậy phương trình chính tắc của elip là \(\frac{{{x^2}}}{{{{120}^2}}} + \frac{{{y^2}}}{{{{100}^2}}} = 1\)
b)
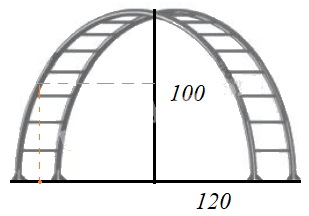
Điểm cách chân 20 cm có hoành độ là \(\left| x \right| = 120 - 20 = 100\)
Thay vào phương trình ta có:
\(\frac{{{{100}^2}}}{{{{120}^2}}} + \frac{{{y^2}}}{{{{100}^2}}} = 1 \Rightarrow {y^2} = {100^2}\left( {1 - \frac{{{{100}^2}}}{{{{120}^2}}}} \right) \Rightarrow y \approx 55\left( {cm} \right)\)
Vậy khoảng cách thẳng đứng từ điểm đó đến khung thép xấp xỉ 55cm.
Bài 4 trang 76 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 76 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Ví dụ 1: Cho hai vectơ \vec{a}" và \vec{b}". Tính \vec{a} + \vec{b}" và \vec{a} - \vec{b}".
Giải:
Để tính \vec{a} + \vec{b}", ta sử dụng quy tắc hình bình hành hoặc quy tắc tam giác. Để tính \vec{a} - \vec{b}", ta có thể sử dụng công thức \vec{a} - \vec{b} = \vec{a} + (-\vec{b})".
Ví dụ 2: Chứng minh rằng \vec{AB} + \vec{BC} = \vec{AC}".
Giải:
Theo quy tắc cộng vectơ, \vec{AB} + \vec{BC}" là vectơ tổng của hai vectơ \vec{AB}" và \vec{BC}". Vectơ tổng này chính là vectơ \vec{AC}".
Khi giải toán vectơ, bạn cần chú ý đến các yếu tố sau:
Để củng cố kiến thức và kỹ năng giải toán vectơ, bạn có thể tự giải các bài tập sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 4 trang 76 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!