Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 117 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách dễ hiểu, cùng với những kiến thức nền tảng cần thiết để nắm vững nội dung chương trình học.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
Hãy cho biết Phương vẽ biểu đồ chính xác chưa. Nếu chưa thì cần điều chỉnh lại như thế nào cho đúng?
Đề bài
Phương vẽ biểu đồ biểu thị tỉ lệ số lượng mỗi loại bếp mà gia đình các bạn trong lớp sử dụng thường xuyên để đun nấu theo bảng thống kê dưới đây:
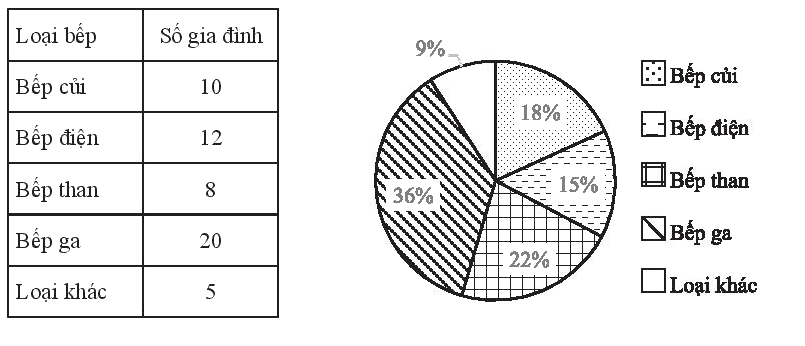
Hãy cho biết Phương vẽ biểu đồ chính xác chưa. Nếu chưa thì cần điều chỉnh lại như thế nào cho đúng?
Lời giải chi tiết
Ta thấy tổng số gia đình các bạn trong lớp là: \(10 + 12 + 8 + 20 + 5 = 55\)
Tỉ số phần trăm từng loại bếp là:
- Bếp củi \(\frac{{10}}{{55}}.100\% \approx 18\% \)
- Bếp điện \(\frac{{12}}{{55}}.100\% \approx 22\% \)
- Bếp than \(\frac{8}{{55}}.100\% \approx 15\% \)
- Bếp ga \(\frac{{20}}{{55}}.100\% \approx 36\% \)
- Loại khác \(\frac{5}{{55}}.100\% \approx 9\% \)
So sánh với biểu đồ, ta thấy Phương vẽ biểu đồ chưa chính xác, Phương nhầm giữa số gia đình dùng bếp điện và gia đình dùng bếp than. Cần điều chỉnh lại phần ghi chú giữa bếp điện và bếp than trên biểu đồ.
Bài 3 trang 117 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và các ứng dụng thực tế.
Bài 3 bao gồm các dạng bài tập sau:
Để giải bài 3 trang 117 sách bài tập Toán 10 Chân trời sáng tạo, học sinh cần nắm vững các kiến thức sau:
Giả sử ta có hai vectơ a = (x1, y1) và b = (x2, y2). Tích vô hướng của a và b được tính như sau:
a.b = x1x2 + y1y2
Ví dụ, nếu a = (2, 3) và b = (-1, 4) thì:
a.b = 2*(-1) + 3*4 = -2 + 12 = 10
Để tìm góc giữa hai vectơ, ta sử dụng công thức:
cos(θ) = (a.b) / (|a||b|)
Sau khi tính được cos(θ), ta sử dụng máy tính hoặc bảng lượng giác để tìm góc θ.
Để chứng minh các đẳng thức vectơ, ta thường sử dụng các tính chất của tích vô hướng và các quy tắc biến đổi vectơ.
Cho tam giác ABC vuông tại A, với AB = 3, AC = 4. Tính tích vô hướng của AB và AC.
Vì tam giác ABC vuông tại A, nên AB vuông góc với AC. Do đó, tích vô hướng của AB và AC bằng 0.
Để củng cố kiến thức, bạn có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 10 Chân trời sáng tạo hoặc các nguồn tài liệu học tập khác.
Bài 3 trang 117 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về tích vô hướng của hai vectơ và các ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan.
| Công thức | Mô tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ |
| |a| = √(x2 + y2) | Độ dài của vectơ |