Bài 5 trang 100 SBT Toán 10 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 100 SBT Toán 10 Chân trời sáng tạo, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
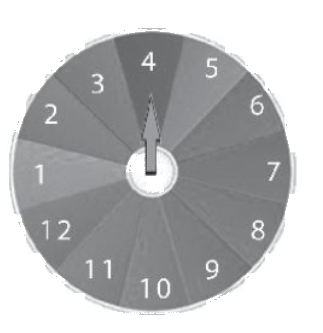
Trên tường có 1 đĩa hình tròn có cấu tạo đồng chất và cân đối. Mặt đĩa được chia thành 12 hình quạt bằng nhau và được đánh số từ 1 đến 12
Đề bài
Trên tường có 1 đĩa hình tròn có cấu tạo đồng chất và cân đối. Mặt đĩa được chia thành 12 hình quạt bằng nhau và được đánh số từ 1 đến 12. Trọng quay đĩa dừng trục gắn ở tâm 3 lần và quan sát xem mỗi khi dừng lại mũi tên chỉ vào ô ghi só mấy. Tính xác suất của các biến cố:
A: “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”
B: “Có đúng 2 lần mũi tên chỉ vào ô ghi số lẻ”
C: “Tích 3 số mũi tên chỉ vào là số nguyên tố”
Phương pháp giải - Xem chi tiết
Phép thử có không gian mẫu gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là 1 biến cố
Xác suất của biến cố A là một số, kí hiệu \(P\left( A \right)\) được xác định bởi công thức: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\), trong đó \(n\left( A \right)\) và \(n\left( \Omega \right)\) lần lượt là kí hiệu số phần tử của tập A và \(\Omega \)
Lời giải chi tiết
Mỗi lần quay, có 12 kết quả có thể xảy ra.
Vậy 3 lần quay, số kết quả có thể xảy ra là: \(n\left( \Omega \right) = 12.12.12 = {12^3}\)
a) Trong 12 số, có 6 số lẻ là: 1; 3; 5; 7; 9; 11
Do đó mỗi lần quay, có 6 trường hợp mũi tên chỉ vào số lẻ.
Số trường hợp để 3 lần quay mũi tên đều chỉ vào số lẻ là: 6.6.6 hay \(n\left( A \right) = {6^3}\)
\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{{6^3}}}{{{{12}^3}}} = \frac{1}{8}\)
b) Để biến cố B xảy ra cần thực hiện 3 công đoạn:
Công đoạn 1: Chọn 2 trong 3 lần (mũi tên chỉ vào số lẻ) => có \(C_3^2\) cách
Công đoạn 2: Hai lần mũi tên chỉ vào số lẻ
Có 6 cách để chỉ vào 1 trong 6 số lẻ, do đó hai lần có: 6.6 =36 cách
Công đoạn 3: Một lần mũi tên chỉ vào số chẵn
Có 6 số chẵn trên bảng, do đó có 6 cách để chỉ vào số chẵn
Theo quy tắc nhân ta có: \(n\left( B \right) = C_3^2.36.6 = 648\)
\( \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{648}}{{{{12}^3}}} = \frac{3}{8}\)
c) Có 5 số nguyên số trong 12 số đã cho là: 2, 3, 5, 7, 11
Để tích 3 số mũi tên chỉ vào là số nguyên tố thì 2 lần quay vào số 1 và 1 lần quay vào 1 trong 5 số nguyên tố đó.
+ Chọn 1 trong 3 lần để quay vào số nguyên tố: có 3 cách
+ Mũi tên quay vào 1 số nguyên tố: Có 5 cách
Theo quy tắc nhân, số kết quả thuận lợi cho biến cố C là: \(n\left( C \right) = 5.3\)
\( \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{5.3}}{{{{12}^3}}} = \frac{5}{{576}}\)
Bài 5 trang 100 SBT Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong không gian. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức về phép cộng, trừ vectơ, tích của một số với vectơ, và các tính chất của vectơ để giải quyết các bài toán liên quan đến hình học không gian.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải bài tập về vectơ hiệu quả, cần nắm vững các kiến thức cơ bản sau:
Để cung cấp lời giải chi tiết, cần biết nội dung cụ thể của bài tập. Tuy nhiên, dưới đây là một ví dụ về cách giải một dạng bài tập thường gặp:
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh AB. Chứng minh rằng: overrightarrow{CM} = (overrightarrow{CA} +overrightarrow{CB})/2
Ta có:
Suy ra: overrightarrow{CA} =overrightarrow{CB} + 2overrightarrow{BM}
Do đó: overrightarrow{CM} =overrightarrow{CA} +overrightarrow{AM} = (overrightarrow{CB} + 2overrightarrow{BM}) +overrightarrow{AM}
Vì overrightarrow{AM} = -overrightarrow{BM} nên:
overrightarrow{CM} =overrightarrow{CB} + 2overrightarrow{BM} -overrightarrow{BM} =overrightarrow{CB} +overrightarrow{BM} = (overrightarrow{CB} +overrightarrow{BA})/2 = (overrightarrow{CA} +overrightarrow{CB})/2 (đpcm)
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em có thể luyện tập thêm các bài tập tương tự trong SBT Toán 10 Chân trời sáng tạo và các tài liệu tham khảo khác.
Vectơ là một khái niệm quan trọng trong toán học, đặc biệt là trong hình học và vật lý. Việc nắm vững kiến thức về vectơ giúp các em học sinh:
Bài 5 trang 100 SBT Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày ở trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.