Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 35 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để nắm vững kiến thức Toán 10 nhé!
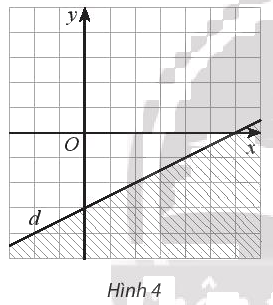
Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong hình 4 (mỗi ô vuông có cạnh là 1 đơn vị)
Đề bài
Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong hình 4 (mỗi ô vuông có cạnh là 1 đơn vị)
Phương pháp giải - Xem chi tiết
Bước 1: Gọi phương trình tổng quát của đường thẳng bờ
Bước 2: Xác định các điểm đường thẳng đi qua và xác định phương trình
Bước 3: Thay tọa độ điểm O(0;0) là nghiệm của bất phương trình cần tìm và xác định dấu của bất phương trình
Lời giải chi tiết
Vì bờ của bất pương trình có dạng là đường thẳng tuyến tính nên phương trình tổng quát có dạng \(y = ax + b\)
Dựa vào hình 4 ta thấy đường thẳng đi qua điểm có tọa độ (6;0) và (0;3)
Thay tọa độ 2 điểm trên vào phương trình tổng quát ta có hệ phương trình hai ẩn như sau: \(\left\{ \begin{array}{l}0 = 6a + b\\3 = 0a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 3\end{array} \right.\)
Vậy phương trình bờ là \(y = - \frac{1}{2}x + 3 \Rightarrow F = \frac{1}{2}x + y - 3\)
Thay \(x = 0,y = 0\) vào phương trình trên ta có \(F = -3 < 0\)
Mặt khác ta thấy gốc tọa độ là nghiệm của bất phương trình (theo hình vẽ) và chứa cả bờ nên ta có bất phương trình cần tìm là \(\frac{1}{2}x + y - 3 \le 0\)
Bài 1 trang 35 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Đây là một bài tập cơ bản, giúp học sinh làm quen với việc xác định các tập hợp con, tập hợp bằng nhau và thực hiện các phép toán hợp, giao, hiệu của hai tập hợp.
Bài tập yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài 1 trang 35 sách bài tập Toán 10 Chân trời sáng tạo, chúng ta cần nắm vững các khái niệm và tính chất cơ bản của tập hợp. Dưới đây là lời giải chi tiết cho từng câu hỏi:
Đề bài: Liệt kê các phần tử của tập hợp A = {x | x là số tự nhiên nhỏ hơn 10}.
Lời giải: Tập hợp A bao gồm các số tự nhiên nhỏ hơn 10, tức là A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Đề bài: Xác định xem hai tập hợp B = {1, 2, 3} và C = {3, 2, 1} có bằng nhau hay không.
Lời giải: Hai tập hợp B và C bằng nhau vì chúng có cùng các phần tử, mặc dù thứ tự liệt kê khác nhau. Tập hợp không quan trọng thứ tự của các phần tử.
Đề bài: Cho hai tập hợp D = {1, 2, 3, 4} và E = {3, 4, 5, 6}. Tìm tập hợp D ∪ E (hợp của D và E).
Lời giải: Tập hợp D ∪ E bao gồm tất cả các phần tử thuộc D hoặc E (hoặc cả hai). Do đó, D ∪ E = {1, 2, 3, 4, 5, 6}.
Đề bài: Cho hai tập hợp D = {1, 2, 3, 4} và E = {3, 4, 5, 6}. Tìm tập hợp D ∩ E (giao của D và E).
Lời giải: Tập hợp D ∩ E bao gồm tất cả các phần tử thuộc cả D và E. Do đó, D ∩ E = {3, 4}.
Đề bài: Cho hai tập hợp D = {1, 2, 3, 4} và E = {3, 4, 5, 6}. Tìm tập hợp D \ E (hiệu của D và E).
Lời giải: Tập hợp D \ E bao gồm tất cả các phần tử thuộc D nhưng không thuộc E. Do đó, D \ E = {1, 2}.
Để giải các bài tập về tập hợp một cách hiệu quả, bạn nên:
Tập hợp có rất nhiều ứng dụng trong thực tế, ví dụ:
Bài 1 trang 35 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10.