Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 3 trang 122 sách bài tập Toán 10 Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích và giải thích rõ ràng để bạn có thể nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau ( đơn vị: mm).
Đề bài
Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).
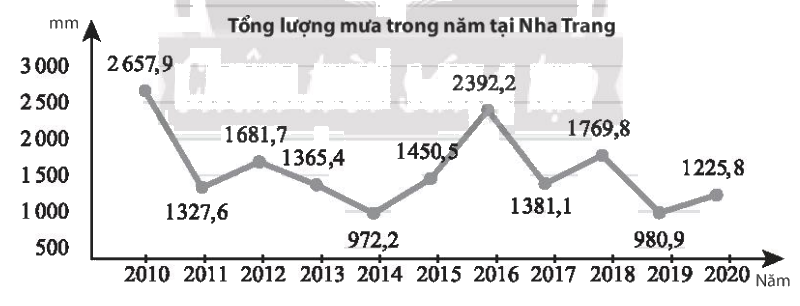
a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020.
b) Hãy tìm các tứ phân vị của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
- Dùng công thức tính số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
- Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Lời giải chi tiết
a) Lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020 là:
\(\overline x = \frac{{2657,9 + 1327,6 + 1681,7 + 1365,4 + 972,2 + 1450,5 + 2392,2 + 1381,1 + 1769,8 + 980,9 + 1225,8}}{{11}} = 1564,1\)
b) Sắp xếp số liệu theo thứ tự không giảm ta được:
972,2 ;980,9; 1225,8; 1327,6; 1365,4; 1381,1; 1450,5; 1681,7; 1769,8; 2392,2; 2657,9.
Vì \(n = 11\)là số lẻ nên \({Q_2} = 1381,1\)
Tứ phân vị thứ nhất là trung vị của 5 số đầu \({Q_1} = 1225,8\)
Tứ phân vị thứ ba là trung vị của 5 số cuối \({Q_3} = 1769,8\)
Bài 3 trang 122 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 3 thường bao gồm các dạng bài tập sau:
Để tìm vectơ tổng a + b, ta cộng tương ứng các tọa độ của hai vectơ a và b. Tương tự, để tìm vectơ hiệu a - b, ta trừ tương ứng các tọa độ của hai vectơ a và b.
Ví dụ: Cho a = (x1, y1) và b = (x2, y2). Khi đó:
Để tìm vectơ tích k.a (với k là một số thực), ta nhân mỗi tọa độ của vectơ a với k.
Ví dụ: Cho a = (x, y) và k là một số thực. Khi đó:
k.a = (kx, ky)
Để chứng minh đẳng thức vectơ, ta có thể sử dụng một trong các phương pháp sau:
Trong các bài toán ứng dụng, cần phân tích kỹ đề bài để xác định các vectơ liên quan và các mối quan hệ giữa chúng. Sau đó, áp dụng các kiến thức đã học để giải quyết bài toán.
Cho A(1; 2), B(3; 4), C(5; 6). Tìm tọa độ của điểm D sao cho AB = DC.
Giải:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 3 trang 122 sách bài tập Toán 10 Chân trời sáng tạo. Chúc bạn học tập tốt!