Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 7 trang 40 sách bài tập Toán 10 Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài tập này với mục tiêu giúp bạn nắm vững kiến thức và kỹ năng giải toán.
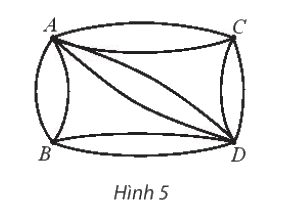
Có các con đường nối bốn ngôi làng A, B, C, D như trong Hình 5.
Đề bài
Có các con đường nối bốn ngôi làng A, B, C, D như trong Hình 5. Có bao nhiêu cách chọn đường đi khác nhau
a) từ A qua B rồi đến D
b) từ A đến D
Lưu ý: Mỗi đường đi qua mỗi ngôi làng ít nhất 1 lần
Lời giải chi tiết
a)
– Từ A qua B có 1 con đường duy nhất: có 1 cách chọn
- Từ B đến D có 1 con đường duy nhất: Có 1 cách chọn
=> Có 1x1 = 1 cách chọn đường
b)
- Cách 1: Từ A đến thẳng D: có 2 con đường: có 2 cách chọn
- Cách 2: Từ A đi qua B hoặc C:
+ Đi qua B hoặc C: Có 2 cách chọn
+ Từ B hoặc C qua D chỉ có 1 con đường: Có 1 cách chọn
=> Có 2x1 = 2 cách chọn
=> Có 2+2 = 4 cách chọn đường
Bài 7 trang 40 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 7 thường bao gồm các dạng bài tập sau:
Để tính tổng hai vectơ \vec{a}" và \vec{b}", ta thực hiện phép cộng theo tọa độ: \vec{a} + \vec{b} = (x_a + x_b, y_a + y_b)". Ví dụ, nếu \vec{a} = (1, 2)" và \vec{b} = (3, -1)" thì \vec{a} + \vec{b} = (4, 1)".
Để tính hiệu hai vectơ \vec{a}" và \vec{b}", ta thực hiện phép trừ theo tọa độ: \vec{a} - \vec{b} = (x_a - x_b, y_a - y_b)". Ví dụ, nếu \vec{a} = (1, 2)" và \vec{b} = (3, -1)" thì \vec{a} - \vec{b} = (-2, 3)".
Để tính tích của một số k" với vectơ \vec{a}", ta nhân số k" với mỗi tọa độ của vectơ \vec{a}": k\vec{a} = (kx_a, ky_a)". Ví dụ, nếu k = 2" và \vec{a} = (1, 2)" thì 2\vec{a} = (2, 4)".
Ví dụ: Cho \vec{a} = (2, -3)" và \vec{b} = (-1, 4)". Tính \vec{a} + \vec{b}" và 3\vec{a}".
Giải:
\vec{a} + \vec{b} = (2 + (-1), -3 + 4) = (1, 1)"
3\vec{a} = (3 \times 2, 3 \times (-3)) = (6, -9)"
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài 7 trang 40 sách bài tập Toán 10 Chân trời sáng tạo một cách dễ dàng và hiệu quả. Hãy luyện tập thêm các bài tập tương tự để củng cố kiến thức và kỹ năng của mình. Chúc bạn học tốt!