Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 5 trang 81 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn dễ dàng theo dõi và hiểu bài.
Hai máy bay rời một sân bay cùng một lúc. Một chiếc máy bay với vận tốc 800 km/h theo hướng lệch so với hướng bắc
Đề bài
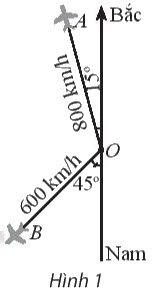
Hai máy bay rời một sân bay cùng một lúc. Một chiếc máy bay với vận tốc 800 km/h theo hướng lệch so với hướng bắc \(15^\circ \) về hướng tây. Chiếc còn lại bay theo hướng lệch so với hướng nam \(45^\circ \) về phía tây với vận tốc 600 km/h (hình 1). Hỏi hai máy bay đó cách nhau bao xa sau 3 giờ?
Lời giải chi tiết
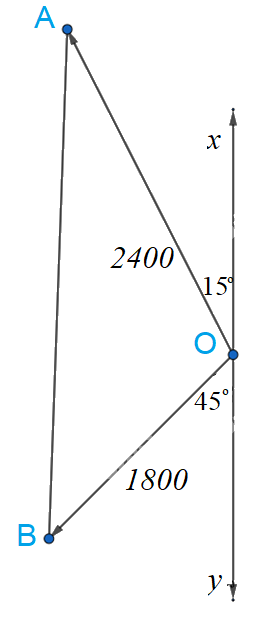
Sau 3 giờ khoảng cách máy bay so với sân bay là: \(OA = 2400\)km, \(OB = 1800\) km
Ta có
\(\widehat {xOA} + \widehat {AOB} + \widehat {BOy} = 180^\circ \Rightarrow \widehat {AOB} = 180^\circ - \left( {\widehat {xOA} + \widehat {BOy}} \right) = 180^\circ - \left( {15^\circ + 45^\circ } \right) = 120^\circ \)
Áp dụng định lí côsin ta có:
\(\begin{array}{l}AB = \sqrt {O{A^2} + O{B^2} - 2OA.OB.\cos \widehat {AOB}} \\ = \sqrt {{{2400}^2} + {{1800}^2} - 2.2400.1800.\cos 120^\circ } \simeq 3649,66\end{array}\)
Vậy khoảng cách của hai máy bay sau 3 giờ là khoảng 3649,66 km
Bài 5 trang 81 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường tập trung vào việc vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan để giải quyết các bài toán hình học và đại số.
Bài 5 thường bao gồm các dạng bài tập sau:
Để tính tổng hai vectơ \vec{a}" và \vec{b}", ta thực hiện phép cộng theo quy tắc hình bình hành hoặc quy tắc tam giác. Nếu biết tọa độ của hai vectơ, ta có thể cộng từng thành phần tương ứng.
Ví dụ: Cho \vec{a} = (x_1, y_1)" và \vec{b} = (x_2, y_2)" thì \vec{a} + \vec{b} = (x_1 + x_2, y_1 + y_2)"
Để tính hiệu hai vectơ \vec{a}" và \vec{b}", ta thực hiện phép trừ theo quy tắc hình bình hành hoặc quy tắc tam giác. Nếu biết tọa độ của hai vectơ, ta trừ từng thành phần tương ứng.
Ví dụ: Cho \vec{a} = (x_1, y_1)" và \vec{b} = (x_2, y_2)" thì \vec{a} - \vec{b} = (x_1 - x_2, y_1 - y_2)"
Để tính tích của một số k" với vectơ \vec{a}", ta nhân số k" với từng thành phần của vectơ \vec{a}".
Ví dụ: Cho \vec{a} = (x, y)" và số k" thì k\vec{a} = (kx, ky)"
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 10 Chân trời sáng tạo hoặc trên các trang web học toán online khác. Ngoài ra, bạn cũng có thể tìm hiểu thêm về các ứng dụng của vectơ trong các lĩnh vực khác như vật lý, kỹ thuật, và khoa học máy tính.
Bài 5 trang 81 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp bạn hiểu rõ hơn về các phép toán vectơ và ứng dụng của chúng. Hy vọng rằng với hướng dẫn chi tiết và các lưu ý quan trọng trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả.