Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 130 sách bài tập Toán 10 Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: 0C)
Đề bài
Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: 0C)
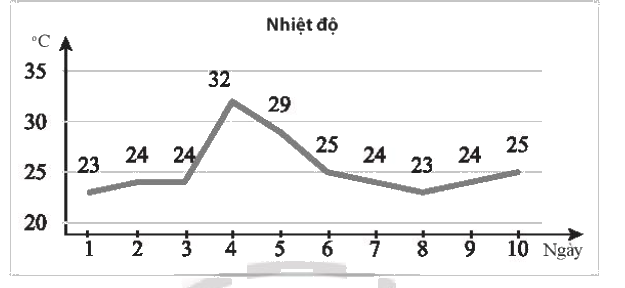
a) Hãy tìm viết mẫu số liệu thống kê nhiệt độ từ biểu đồ trên.
b) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.
c) Hãy tìm phương sai và độ lệch chuẩn của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
Sắp xếp số liệu theo thứ tự không giảm và tìm khoảng biến thiên theo công thức\(R = {x_n} - {x_1}\)
Dùng kiến thức khoảng biến thiên và khoảng tứ phân vị, giá trị ngoại lệ đã học.
Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2} \right) - {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)
Lời giải chi tiết
a) Mẫu số liệu:
Nhiệt độ | 23 | 23 | 24 | 24 | 24 | 24 | 25 | 25 | 29 | 32 |
b)
+ Số cao nhất và thấp nhất lần lượt là 32 và 23 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 32 - 23 = 9\)
+ Tứ phân vị: \({Q_2} = 24\); \({Q_1} = 24;{Q_3} = 25 \Rightarrow \Delta Q = {Q_3} - {Q_1} = 1\)
c)
+ Trung bình của mẫu số liệu là \(\overline x = 25,3\)
+ Phương sai: \({S^2} = 7,61\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} \approx 2,76\)
Bài 4 trang 130 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, và các tính chất của hàm số bậc hai để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài tập này, bạn có thể áp dụng các phương pháp sau:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng câu hỏi cụ thể trong bài tập. Dưới đây là một ví dụ minh họa:
Cho hàm số f(x) = 2x2 - 5x + 3. Hãy tìm:
1. Tập xác định: Vì hàm số f(x) = 2x2 - 5x + 3 là một hàm đa thức bậc hai, nên tập xác định của hàm số là tập số thực, ký hiệu là R.
2. Tập giá trị: Hàm số f(x) = 2x2 - 5x + 3 là một hàm bậc hai có hệ số a = 2 > 0, do đó parabol có dạng mở lên trên. Giá trị nhỏ nhất của hàm số đạt được tại đỉnh của parabol. Hoành độ đỉnh là x = -b / 2a = -(-5) / (2 * 2) = 5/4. Tung độ đỉnh là f(5/4) = 2 * (5/4)2 - 5 * (5/4) + 3 = -7/8. Vậy tập giá trị của hàm số là [-7/8, +∞).
3. Tọa độ đỉnh: Tọa độ đỉnh của parabol là (5/4, -7/8).
Ngoài bài 4, sách bài tập Toán 10 Chân trời sáng tạo còn có nhiều bài tập tương tự về hàm số bậc hai. Để giải các bài tập này, bạn cần nắm vững các kiến thức và phương pháp đã trình bày ở trên. Hãy luyện tập thường xuyên để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Bài 4 trang 130 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc hai. Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập đã trình bày, bạn sẽ tự tin hơn khi giải các bài toán tương tự. Chúc bạn học tập tốt!