Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn cách giải bài 2 trang 21 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập mới. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết và dễ tiếp thu nhất.
Xét dấu của các tam thức bậc hai sau:
Đề bài
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = - 7{x^2} + 44x - 45\) b) \(f\left( x \right) = 4{x^2} + 36x + 81\)
c) \(f\left( x \right) = 9{x^2} - 6x + 3\) d) \(f\left( x \right) = - 9{x^2} + 30x - 25\)
e) \(f\left( x \right) = - {x^2} - 4x + 3\) g) \(f\left( x \right) = - 4{x^2} + 8x - 7\)
Lời giải chi tiết
a) \(f\left( x \right) = - 7{x^2} + 44x - 45\) có \(\Delta = 676 > 0\), hai nghiệm \({x_1} = \frac{9}{7};{x_2} = 5\) và có \(a = - 7 < 0\)
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
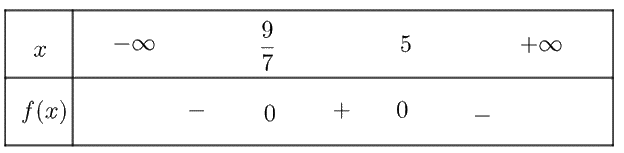
Vậy \(f\left( x \right)\) dương trong khoảng \(\left( {\frac{9}{7};5} \right)\) và âm trong khoảng \(\left( { - \infty ;\frac{9}{7}} \right) \cup \left( {5; + \infty } \right)\)
b) \(f\left( x \right) = 4{x^2} + 36x + 81\) có \(\Delta = 0\), nghiệm kép \({x_1} = {x_2} = - \frac{9}{2}\) và có \(a = 4 > 0\)
nên \(f\left( x \right)\) luôn dương với \(x \ne - \frac{9}{2}\)
Vậy \(f\left( x \right)\) dương trong khoảng \(\mathbb{R}\backslash \left\{ { - \frac{9}{2}} \right\}\)
c) \(f\left( x \right) = 9{x^2} - 6x + 3\) có \(\Delta = - 72 < 0\) và\(a = 9 > 0\)
nên \(f\left( x \right)\) luôn dương với mọi \(x \in \mathbb{R}\)
Vậy \(f\left( x \right)\) dương với mọi x
d) \(f\left( x \right) = - 9{x^2} + 30x - 25\) có \(\Delta = 0\), nghiệm kép \({x_1} = {x_2} = \frac{5}{3}\) và có \(a = - 9 < 0\)
nên \(f\left( x \right)\) luôn âm với \(x \ne \frac{5}{3}\)
Vậy \(f\left( x \right)\) âm trong khoảng \(\mathbb{R}\backslash \left\{ {\frac{5}{3}} \right\}\)
e) \(f\left( x \right) = {x^2} - 4x + 3\) có \(\Delta = 4 > 0\), hai nghiệm \({x_1} = 1;{x_2} = 3\) và có \(a = 1 > 0\)
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
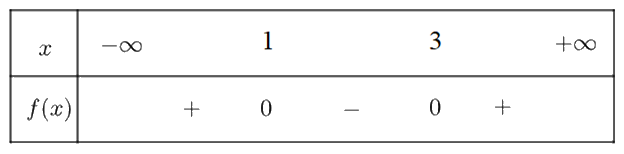
Vậy \(f\left( x \right)\) dương trên khoảng \(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\) và âm trong khoảng \(\left( {1;3} \right)\)
g) \(f\left( x \right) = - 4{x^2} + 8x - 7\) có có \(\Delta = - 48 < 0\) và\(a = - 4 < 0\)
nên \(f\left( x \right)\) luôn âm với mọi \(x \in \mathbb{R}\)
Bài 2 trang 21 SBT Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử của tập hợp, tập con, tập rỗng, và các phép toán hợp, giao, hiệu của hai tập hợp để giải quyết các bài toán cụ thể.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải bài tập về tập hợp hiệu quả, bạn có thể áp dụng các phương pháp sau:
Bài 2a: Cho A = {0; 1; 2; 3; 4; 5}. Hãy liệt kê các tập con của A có 3 phần tử.
Lời giải: Các tập con của A có 3 phần tử là:
Bài 2b: Cho B = {1; 2; 3}. Hãy liệt kê các tập con của B.
Lời giải: Các tập con của B là:
Ví dụ: Cho C = {a; b; c; d}. Tìm tập hợp D gồm các phần tử là các tập con của C có đúng 2 phần tử.
Lời giải: Tập hợp D là:
D = {{a; b}, {a; c}, {a; d}, {b; c}, {b; d}, {c; d}}
Để củng cố kiến thức về tập hợp và các phép toán trên tập hợp, bạn có thể tự giải thêm các bài tập sau:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 2 trang 21 SBT Toán 10 Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!