Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 5 trang 97 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp và cách tiếp cận bài toán.
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Đề bài
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Lời giải chi tiết
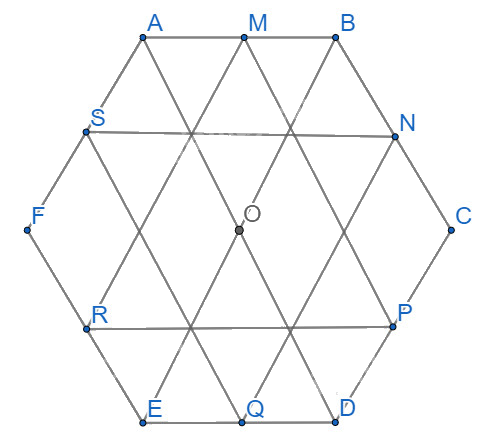
Gọi O là trọng tâm của tam giác MPR
Ta có MN là đường trung bình của tam giác ABC nên \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \)
Tương tự PQ và RS cũng là đường trung bình của tam giác CDE và EFA nên
\(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CE} ;\overrightarrow {RS} = \frac{1}{2}\overrightarrow {EA} \)
Từ đó suy ra \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {CE} + \frac{1}{2}\overrightarrow {EA} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right) = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 \)
\( \Leftrightarrow \left( {\overrightarrow {MO} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {PO} + \overrightarrow {OQ} } \right) + \left( {\overrightarrow {RO} + \overrightarrow {OS} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {ON} + \overrightarrow {OQ} + \overrightarrow {OS} = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} \)
Mà ta có O là trọng tâm của tam giác MPR nên \(\overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} = \overrightarrow 0 \)
Suy ra \(\overrightarrow {ON} + \overrightarrow {OQ} + \overrightarrow {OS} = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} = \overrightarrow 0 \)
Vậy O vừa trọng tâm của tam giác MPR vừa là trọng tâm của tam giác NQS
Bài 5 trang 97 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập: Bài 5 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, tìm tọa độ đỉnh, trục đối xứng và vẽ đồ thị hàm số.
Để xác định hệ số a, b, c của hàm số bậc hai, học sinh cần đưa hàm số về dạng tổng quát y = ax² + bx + c. Sau đó, so sánh với dạng tổng quát để xác định giá trị của a, b, c.
Ví dụ: Cho hàm số y = 2x² - 5x + 3. Ta có:
Tọa độ đỉnh của parabol có dạng (x₀; y₀), trong đó:
Ví dụ: Với hàm số y = 2x² - 5x + 3, ta có:
Vậy tọa độ đỉnh của parabol là (5/4; -7/8).
Trục đối xứng của parabol là đường thẳng có phương trình x = x₀, trong đó x₀ là hoành độ của đỉnh parabol.
Ví dụ: Với tọa độ đỉnh (5/4; -7/8), trục đối xứng của parabol là x = 5/4.
Để vẽ đồ thị hàm số bậc hai, ta thực hiện các bước sau:
Lưu ý:
Bài tập tương tự: Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Kết luận: Bài 5 trang 97 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và các tính chất của nó. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ là nền tảng vững chắc cho việc học tập các kiến thức toán học nâng cao hơn.