Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn cách giải câu 4 trang 19 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
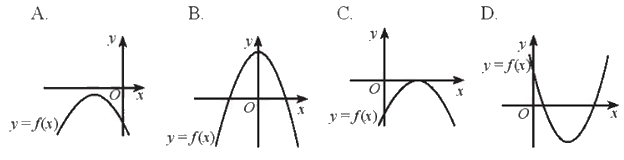
Trong trường hợp nào tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) có \(\Delta > 0\) và \(a < 0\)?
Đề bài
Trong trường hợp nào tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) có \(\Delta > 0\) và \(a < 0\)?
Phương pháp giải - Xem chi tiết
Hàm số có \(a < 0\) là hàm số có đồ thị quay bề lõm về phía dưới và \(\Delta > 0\) khi và chỉ khi hàm số có hai nghiệm phân biệt tương đương cắt trục hoành tại hai điểm phân biệt
Lời giải chi tiết
Hàm số có \(a < 0\) là hàm số có đồ thị quay bề lõm về phía dưới và \(\Delta > 0\) khi và chỉ khi hàm số có hai nghiệm phân biệt tương đương cắt trục hoành tại hai điểm phân biệt
Chọn B.
Câu 4 trang 19 SBT Toán 10 Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về tập hợp số, các phép toán trên tập hợp và biểu diễn tập hợp bằng sơ đồ Venn để giải quyết bài toán thực tế. Bài toán này thường liên quan đến việc xác định các phần tử thuộc, không thuộc một tập hợp cho trước, hoặc tìm số lượng phần tử trong một tập hợp dựa trên các thông tin đã cho.
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn tránh sai sót và tìm ra phương pháp giải phù hợp. Trong câu 4 trang 19, bạn cần xác định rõ các tập hợp được đề cập, các phần tử thuộc mỗi tập hợp và mối quan hệ giữa chúng.
Để giải quyết bài toán, bạn cần nắm vững các khái niệm cơ bản về tập hợp, bao gồm:
Sơ đồ Venn là một công cụ hữu ích để minh họa các tập hợp và mối quan hệ giữa chúng. Bạn có thể sử dụng sơ đồ Venn để biểu diễn các tập hợp, các phần tử thuộc mỗi tập hợp và các phép toán trên tập hợp. Điều này giúp bạn dễ dàng hình dung và giải quyết bài toán.
Giả sử đề bài yêu cầu tìm số lượng học sinh thích học Toán và Văn trong một lớp học. Bạn có thể sử dụng sơ đồ Venn để biểu diễn tập hợp học sinh thích Toán (T) và tập hợp học sinh thích Văn (V). Phần giao của hai tập hợp (T ∩ V) sẽ biểu diễn số lượng học sinh thích cả hai môn học.
Câu 4 trang 19 SBT Toán 10 Chân trời sáng tạo có thể xuất hiện dưới nhiều dạng khác nhau, bao gồm:
Để nắm vững kiến thức về tập hợp và rèn luyện kỹ năng giải bài tập, bạn nên luyện tập thường xuyên với các bài tập khác trong sách bài tập và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán để được hướng dẫn chi tiết hơn.
Dưới đây là một số lời khuyên giúp bạn giải bài tập câu 4 trang 19 SBT Toán 10 Chân trời sáng tạo một cách hiệu quả:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết câu 4 trang 19 SBT Toán 10 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!