Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách Giải bài 4 trang 27 sách bài tập Toán 10 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập mới. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích dễ hiểu để giúp bạn nắm vững kiến thức.
Bạn Nga muốn pha 2 loại nước rửa xe. Để pha 1 lít loại I cần 600 ml dung dịch chất tẩy rửa, còn loại II chỉ cần 400 ml.
Đề bài
Bạn Nga muốn pha 2 loại nước rửa xe. Để pha 1 lít loại I cần 600 ml dung dịch chất tẩy rửa, còn loại II chỉ cần 400 ml. Gọi x và y lần lượt là số lít nước rửa xe loại I và loại II pha chế được và biết rằng Nga chỉ còn 2 400ml chất tẩy rửa, hãy lập các bất phương trình mô tả số lít nước rửa xe loại I và II mà bạn Nga có thể pha chế được và biểu diễn miền nghiệm của từng bất phương trình đó trên mặt phẳng tọa độ Oxy
Lời giải chi tiết
Do x, y lần lượt là số lít nước rửa xe loại I và II pha chế được nên x ≥ 0, y ≥ 0.
Để pha chế x lít nước rửa xe loại I, Nga cần số ml dung dịch chất tẩy rửa là: 600x (ml).
Để pha chế y lít nước rửa xe loại II, Nga cần số ml dung dịch chất tẩy rửa là: 400y (ml).
Tổng số ml dung dịch chất tẩy rửa Nga dùng để pha chế x lít nước rửa xe loại I và y lít nước rửa xe loại II là 600x + 400y.
Mà Nga chỉ có 2 400 ml dung dịch chất tẩy rửa nên 600x + 400y ≤ 2 400 ⇔ 3x + 2y ≤ 12.
Vậy các bất phương trình mô tả số lít nước rửa xe loại I và loại II mà bạn Nga có thể pha chế được là: x ≥ 0, y ≥ 0, 3x + 2y ≤ 12.
Ta biểu diễn miền nghiệm của các bất phương trình trên.
Vẽ đường thẳng \(d:3x + 2y = 12\) đi qua hai điểm \(A\left( {0;6} \right)\) và \(B\left( {4;0} \right)\)
Xét gốc tọa độ \(O\left( {0;0} \right)\)
Ta thấy \(O \notin d\) và \(3.0 + 2.0 = 0 < 12\). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ d vàchứa gốc tọa độ O (miền không gạch chéo như hình dưới)
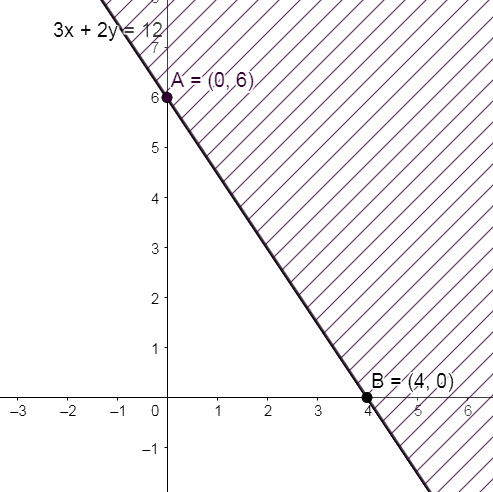
Bài 4 trang 27 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử của tập hợp, tập con, tập hợp rỗng, và các phép toán hợp, giao, hiệu, bù để giải quyết các bài toán cụ thể.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 27 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Ví dụ 1: Cho A = {1, 2, 3}, B = {2, 4, 5}. Tìm A ∪ B, A ∩ B, A \ B.
Giải:
Ví dụ 2: Chứng minh A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
Giải:
Để chứng minh đẳng thức này, ta cần chứng minh hai chiều:
Khi giải các bài tập về tập hợp, bạn cần chú ý:
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 4 trang 27 sách bài tập Toán 10 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong môn Toán.
| Phép toán | Ký hiệu | Định nghĩa |
|---|---|---|
| Hợp | A ∪ B | Tập hợp chứa tất cả các phần tử thuộc A hoặc thuộc B. |
| Giao | A ∩ B | Tập hợp chứa tất cả các phần tử thuộc cả A và B. |
| Hiệu | A \ B | Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. |
| Bù | CAB | Tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A. |