Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 5 trang 19, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc \(60^\circ \) đến vị trí A sau đó đi tiếp 3 m đến vị trí B như hình 1.
Đề bài
Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc \(60^\circ \) đến vị trí A sau đó đi tiếp 3 m đến vị trí B như hình 1.
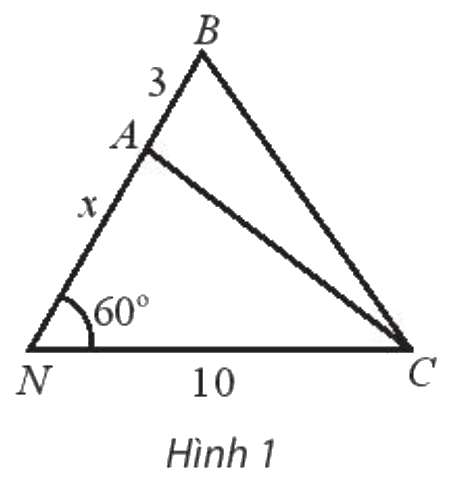
a) Biểu diễn khoảng cách AC và BC theo x
b) Tìm x để \(AC = \frac{8}{9}BC\)
c) Tìm x để khoảng cách \(BC = 2AN\)
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí côsin \(a = \sqrt {{b^2} + {c^2} - 2bc\cos A} \)
b) Lập phương trình dựa vào kết quả của câu a) và giải phương trình
c) Lập phương liên quan và giải phương trình
Lời giải chi tiết
a) Áp dụng đính lí côsin trong tam giác ANC ta có:
\(\begin{array}{l}AC = \sqrt {A{N^2} + N{C^2} - 2AN.NC.\cos \widehat N} = \sqrt {{x^2} + {{10}^2} - 2x.10.\cos 60^\circ } \\ = \sqrt {{x^2} - 10x + 100} \end{array}\)
Áp dụng đính lí côsin trong tam giác BNC ta có:
\(\begin{array}{l}BC = \sqrt {B{N^2} + N{C^2} - 2BN.NC.\cos \widehat N} = \sqrt {{{\left( {x + 3} \right)}^2} + {{10}^2} - 2\left( {x + 3} \right).10.\cos 60^\circ } \\ = \sqrt {{x^2} - 4x + 79} \end{array}\)
b) Ta có: \(AC = \frac{8}{9}BC\) hay
\(\begin{array}{l}\sqrt {{x^2} - 10x + 100} = \frac{8}{9}\sqrt {{x^2} - 4x + 79} \\ \Rightarrow {x^2} - 10x + 100 = \frac{{64}}{{81}}\left( {{x^2} - 4x + 79} \right)\\ \Rightarrow \frac{{17}}{{81}}{x^2} - \frac{{554}}{{81}}x + \frac{{3044}}{{81}} = 0\end{array}\)
\( \Rightarrow x \simeq 7\) hoặc \(x \simeq 25,6\)
Thay hai giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn
Vậy khi \(x \simeq 7\) hoặc \(x \simeq 25,6\) thì \(AC = \frac{8}{9}BC\)
c) Yêu cầu bài toán tương đương
\(\begin{array}{l}\sqrt {{x^2} - 4x + 79} = 2x\\ \Rightarrow {x^2} - 4x + 79 = 4{x^2}\\ \Rightarrow 3{x^2} + 4x - 79 = 0\end{array}\)
\( \Rightarrow x = \frac{{ - 2 - \sqrt {241} }}{3}\) hoặc \(x = \frac{{ - 2 + \sqrt {241} }}{3}\)
Mà vì \(x \ge 0\) nên \(x = \frac{{ - 2 + \sqrt {241} }}{3}\)
Vậy khi \(x = \frac{{ - 2 + \sqrt {241} }}{3}\) thì \(BC = 2AN\)
Bài 5 trang 19 SBT Toán 10 Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp. Bài tập này thường yêu cầu học sinh xác định các tập hợp con, tìm giao điểm, hợp, hiệu của các tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 5 thường bao gồm các câu hỏi và bài tập sau:
Để giải các bài tập về tập hợp một cách hiệu quả, bạn cần nắm vững các kiến thức và kỹ năng sau:
Dưới đây là giải chi tiết từng phần của bài 5 trang 19 SBT Toán 10 Chân trời sáng tạo. (Lưu ý: Vì nội dung bài tập cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa)
Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm:
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, bạn có thể luyện tập thêm với các bài tập sau:
Để học tập môn Toán hiệu quả, bạn nên:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 5 trang 19 SBT Toán 10 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!