Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 34 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Cho biết mỗi kilogam thịt bò giá 250 nghìn đồng, trong đó có chứa khoảng 800 đơn vị protein và 100 đơn vị lipit, mỗi kilogam thịt heo có giá 200 nghìn đồng, trong đo có chứa khoảng 600 đơn vị protein và 200 đơn vị lipit.
Đề bài
Cho biết mỗi kilogam thịt bò giá 250 nghìn đồng, trong đó có chứa khoảng 800 đơn vị protein và 100 đơn vị lipit, mỗi kilogam thịt heo có giá 200 nghìn đồng, trong đo có chứa khoảng 600 đơn vị protein và 200 đơn vị lipit. Một gia đình cần ít nhất 800 đơn vị protein và 200 đơn vị lipit trong khẩu phần thức ăn mỗi ngày và họ chỉ có thể mua một ngày không quá 1 kg thịt bò và 1,5 kg thịt heo. Hỏi gia đình này phải mua bao nhiêu kilogam thịt mỗi loại để chi phí là ít nhất
Lời giải chi tiết
Gọi x,y là số kilogam thịt bò và thịt lợn mà gia đình đó mua.
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
\(\left\{ \begin{array}{l}800x + 600y \ge 800\\100x + 200y \ge 200\\0 \le x \le 1\\0 \le y \le 1,5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 3y \ge 4\\x + 2y \ge 2\\x \ge 0\\x \le 1\\y \ge 0\\y \le 1,5\end{array} \right.\)
Biểu diễn miền nghiệm của hệ phương trình trên hệ trục tọa độ Oxy ta được miền nghiệm đa giác ABCDE. Tọa độ các đỉnh của đa giác như hình vẽ:
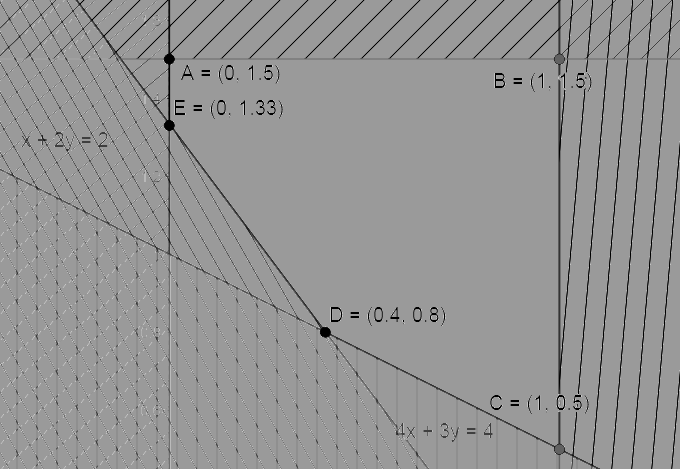
Gọi F là chi phí gia đình sử dụng mua thịt (đơn vị: nghìn đồng), ta có: \(F = 250x + 200y\)
Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho F nhỏ nhất, nghĩa là tìm giá trị nhỏ nhất của \(F = 250x + 200y\) trên miền đa giác ABCDE
Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có:
Tại \(A\left( {0;\frac{3}{2}} \right)\): \(F = 250.0 + 200.\frac{3}{2} = 300\)
Tại \(B\left( {1;\frac{3}{2}} \right)\): \(F = 250.1 + 200.\frac{3}{2} = 550\)
Tại \(C\left( {1;\frac{1}{2}} \right)\): \(F = 250.1 + 200.\frac{1}{2} = 350\)
Tại \(D\left( {\frac{2}{5};\frac{4}{5}} \right)\): \(F = 250.\frac{2}{5} + 200.\frac{4}{5} = 260\)
Tại \(E\left( {0;\frac{4}{3}} \right)\): \(F = 250.0 + 200.\frac{4}{3} \simeq 266,67\)
Vậy ta thấy tại đỉnh \(D\left( {\frac{2}{5};\frac{4}{5}} \right)\) thì giá trị F nhỏ nhất
Vậy khi gia đình đó mua 0,4 kg thịt bò và 0,8 kg thịt lợn mỗi ngày để vẫn đủ lượng protein và lipit và chi phí nhỏ nhất là 260 nghìn đồng
Bài 4 trang 34 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử của tập hợp, tập con, tập rỗng, và các phép toán hợp, giao, hiệu, bù để giải quyết các bài toán cụ thể.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 4 trang 34, chúng ta sẽ đi vào phân tích từng phần của bài tập.
(Giả sử đề bài là: Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm A ∪ B)
Để tìm hợp của hai tập hợp A và B (ký hiệu là A ∪ B), ta cần liệt kê tất cả các phần tử thuộc A hoặc B (hoặc cả hai).
A ∪ B = {1, 2, 3, 4, 5, 6, 7}
(Giả sử đề bài là: Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm A ∩ B)
Để tìm giao của hai tập hợp A và B (ký hiệu là A ∩ B), ta cần liệt kê các phần tử thuộc cả A và B.
A ∩ B = {3, 4, 5}
(Giả sử đề bài là: Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm A \ B)
Để tìm hiệu của hai tập hợp A và B (ký hiệu là A \ B), ta cần liệt kê các phần tử thuộc A nhưng không thuộc B.
A \ B = {1, 2}
(Giả sử đề bài là: Cho A = {1, 2, 3, 4, 5} và U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Hãy tìm A')
Để tìm phần bù của tập hợp A trong tập hợp U (ký hiệu là A'), ta cần liệt kê các phần tử thuộc U nhưng không thuộc A.
A' = {6, 7, 8, 9, 10}
Kiến thức về tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Bài 4 trang 34 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.