Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 101 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 10 nhé!
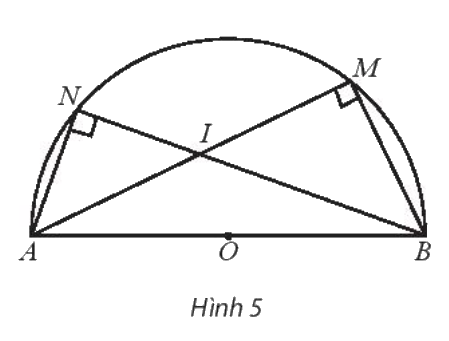
Cho nửa đường tròn tâm O có đường kính AB = 2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như hình 5.
Đề bài
Cho nửa đường tròn tâm O có đường kính \(AB = 2R\). Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như hình 5.
a) Chứng minh: \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB} ;\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AB} .\overrightarrow {BA} \)
b) Tính \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} \) theo R
Lời giải chi tiết
a) Ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} = \left| {\overrightarrow {AI} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AI} ,\overrightarrow {AM} } \right)\\ = AI.AM.\cos 0^\circ = AI.AM\end{array}\) (*)
Mặt khác \(AM = AB.\cos \widehat {MAB}\), thay vào (*) ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} = AI.AM = AI.AB.\cos \widehat {MAB}\\ = \left| {\overrightarrow {AI} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AI} ,\overrightarrow {AB} } \right) = \overrightarrow {AI} .\overrightarrow {AB} \end{array}\) (đpcm)
\(\begin{array}{l}\overrightarrow {BI} .\overrightarrow {BN} = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BN} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BN} } \right)\\ = BI.BN.\cos 0^\circ = BI.BN\end{array}\) (**)
Mặt khác \(BN = BA.\cos \widehat {NBA}\), thay vào (**) ta có:
\(\begin{array}{l}\overrightarrow {BI} .\overrightarrow {BN} = BI.BN = BI.BA.\cos \widehat {NBA}\\ = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BA} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BA} } \right) = \overrightarrow {BI} .\overrightarrow {BA} \end{array}\) (đpcm)
b) Từ kết quả của câu a) ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\\ = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {AB} .\overrightarrow {BI} = \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) = \overrightarrow {AB} \left( {\overrightarrow {AI} + \overrightarrow {IB} } \right) = {\overrightarrow {AB} ^2}\\ = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\end{array}\)
Vậy \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = 4{R^2}\)
Bài 3 trang 101 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là phép cộng, trừ vectơ và phép nhân vectơ với một số thực để giải quyết các bài toán cụ thể. Việc nắm vững các định nghĩa, tính chất và quy tắc thực hiện các phép toán vectơ là chìa khóa để giải quyết thành công bài tập này.
Bài 3 bao gồm một số câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Để thực hiện các phép toán vectơ, học sinh cần nhớ rõ quy tắc cộng, trừ vectơ. Cụ thể:
Ví dụ: Cho hai vectơ a = (1; 2) và b = (3; -1). Tính a + b và a - b.
Giải:
Trong các bài tập hình học, vectơ được sử dụng để biểu diễn các đoạn thẳng, đường thẳng, và các mối quan hệ giữa chúng. Việc sử dụng vectơ giúp đơn giản hóa việc giải quyết các bài toán hình học phức tạp.
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AM = AB + AC / 2.
Giải:
Vì M là trung điểm của BC, ta có BM = MC. Do đó, AM = AB + BM = AB + BC / 2 = AB + (AC - AB) / 2 = AB + AC / 2 - AB / 2 = AB + AC / 2.
Bài 3 trang 101 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán.