Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 6 trang 55 sách bài tập Toán 10 Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như hình 11
Đề bài
Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như hình 11
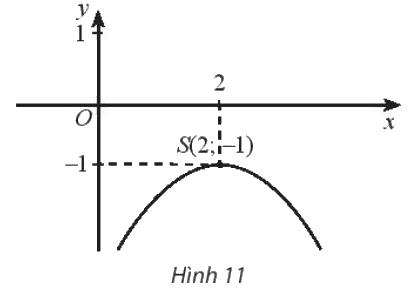
Lời giải chi tiết
Hàm số có đồ thị là một parabol nê đó là hàm số bậc hai, suy có có tập xác định \(D = \mathbb{R}\)
Từ đồ thị hàm số ta thấy rằng, parabol quay bề lõm xuống dưới và có đỉnh \(S\left( {2; - 1} \right)\) nên có bảng biến thiên như sau:
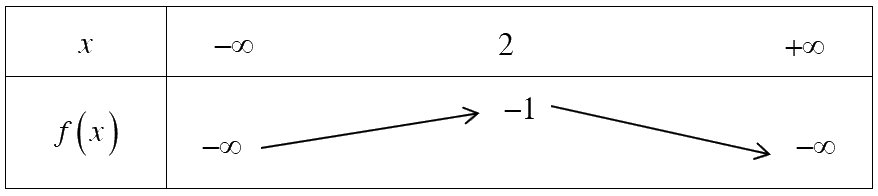
Từ bảng biến thiên ta có: giá trị lớn nhất của hàm số là \( - 1\), tập giá trị của hàm số là \(T = \left( { - \infty ; - 1} \right]\), đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và nghịch biến trên khoảng \(\left( { - 1; + \infty } \right)\)
Bài 6 trang 55 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 55 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản về vectơ và các phép toán vectơ. Dưới đây là hướng dẫn chi tiết cho từng dạng bài tập:
Để thực hiện các phép toán vectơ, bạn cần nhớ các quy tắc sau:
Ví dụ: Cho hai vectơ a = (2, 3) và b = (-1, 4). Tính a + b và 2a.
Lời giải:
Để chứng minh đẳng thức vectơ, bạn cần sử dụng các tính chất của phép cộng, phép trừ vectơ, tích của một số với vectơ để biến đổi vế trái thành vế phải (hoặc ngược lại).
Ví dụ: Chứng minh rằng a + b = b + a với mọi vectơ a và b.
Lời giải:
Ta có: a + b = (ax + bx, ay + by) và b + a = (bx + ax, by + ay). Vì phép cộng các số thực có tính giao hoán nên ax + bx = bx + ax và ay + by = by + ay. Do đó, a + b = b + a.
Khi ứng dụng vectơ vào hình học, bạn cần sử dụng vectơ để biểu diễn các điểm, đường thẳng, và các mối quan hệ giữa chúng. Ví dụ, bạn có thể sử dụng vectơ để chứng minh hai đường thẳng song song, hai tam giác bằng nhau, hoặc một điểm nằm trên một đường thẳng.
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 6 trang 55 sách bài tập Toán 10 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải toán vectơ nhé!