Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 7 trang 75 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của các bạn.
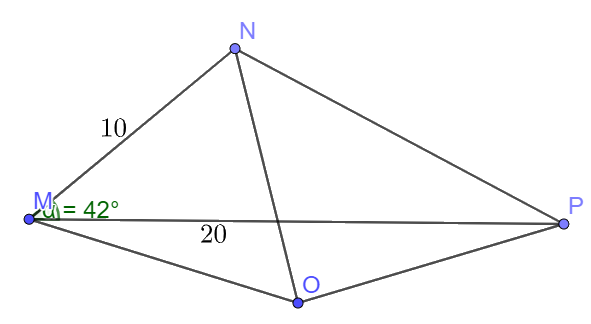
a) Tính diện tích tam giác MNP b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP
Đề bài
Cho tam giác MNP có \(MN = 10,MP = 20\)và \(\widehat M = 42^\circ \)
a) Tính diện tích tam giác MNP
b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP
Lời giải chi tiết
a) Ta có công thức \(S = \frac{1}{2}ab\sin C = \frac{1}{2}.MN.MP.\sin M\)
\( = \frac{1}{2}.10.20.\sin 42^\circ \simeq 66,91\) (đvdt)
b) O là tâm đường tròn ngoại tiếp tam giác MNP nên ta có:
\(OM = ON = OP = R = \frac{{NP}}{{2\sin M}}\) (*)
Áp dụng định lí côsin ta tính được NP như sau:
\(NP = \sqrt {M{P^2} + M{N^2} - 2.MP.MN.\cos M} \simeq 14,24\) (cm)
Thay NP vừa tính được vào (*) ta có:
\(OM = ON = OP = R = \frac{{NP}}{{2\sin M}} = \frac{{14,24}}{{2.\sin 42^\circ }} \simeq 10,64\)
Tam giác ONP có \(ON = OP = 10,64;NP = 14,24\)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \simeq 56,3\)(cm2)
Bài 7 trang 75 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường tập trung vào việc vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan để giải quyết các bài toán hình học và đại số cơ bản.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giải các bài toán tính toán vectơ, các em cần nắm vững các quy tắc sau:
Ví dụ: Cho a = (2, 3) và b = (-1, 4). Tính a + b và 2a.
a + b = (2 - 1, 3 + 4) = (1, 7)
2a = (2*2, 2*3) = (4, 6)
Để chứng minh đẳng thức vectơ, các em có thể sử dụng các phương pháp sau:
Ví dụ: Chứng minh rằng a + b = b + a với mọi vectơ a và b.
Ta có: a + b = (ax + bx, ay + by) = (bx + ax, by + ay) = b + a. Vậy đẳng thức được chứng minh.
Đối với các bài toán ứng dụng, các em cần phân tích kỹ đề bài để xác định các vectơ liên quan và các mối quan hệ giữa chúng. Sau đó, sử dụng các kiến thức đã học để giải quyết bài toán.
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AM = (AB + AC)/2.
Giải: Ta có AM = (AB + AC)/2 là một kết quả quen thuộc trong hình học vectơ. Các em có thể chứng minh bằng cách sử dụng quy tắc trung điểm hoặc bằng cách sử dụng tọa độ vectơ.
Bài 7 trang 75 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về vectơ. Hy vọng với hướng dẫn chi tiết này, các em sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc các em học tốt!