Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 17 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp và cách tiếp cận bài toán.
Lớp 10E có 18 bạn chơi cầu lông, 15 bạn chơi cờ vua, 10 bạn chơi cả hai môn và 12 bạn không chơi môn nào trong hai môn thể thao này
Đề bài
Lớp 10E có 18 bạn chơi cầu lông, 15 bạn chơi cờ vua, 10 bạn chơi cả hai môn và 12 bạn không chơi môn nào trong hai môn thể thao này
a) Lớp 10E có bao nhiêu bạn chơi ít nhất một môn thể thao trên?
b) Lớp 10E có bao nhiêu học sinh?
Lời giải chi tiết
Tập hợp A là tập hợp 18 bạn chơi cầu lông
Tập hợp B là tập hợp 15 bạn chơi cờ vua
Tập hợp C là tập hợp các bạn không chơi môn nào trong hai môn thể thao này
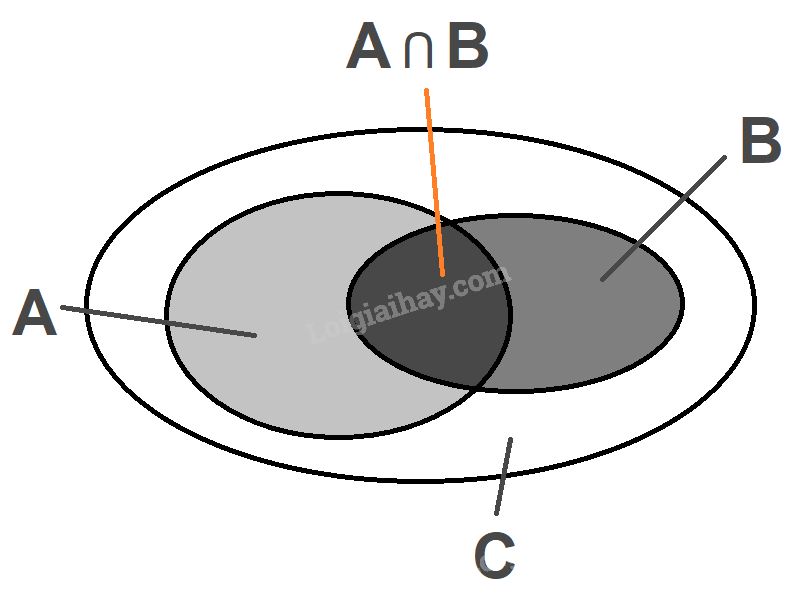
Theo giả thiết ta có: \(n\left( {A \cap B} \right) = 10\)
Tập hợp các bạn chỉ chơi cầu lông là \(n\left( {A\backslash \left( {A \cap B} \right)} \right) = 8\)
Tập hợp các bạn chỉ chơi cờ vua là \(n\left( {B\backslash \left( {A \cap B} \right)} \right) = 5\)
a) Tập hợp các bạn chơi ít nhất 1 môn thể thao là \(n\left( {A \cap B} \right) + n\left( {A\backslash B} \right) + n\left( {B\backslash A} \right) = 10 + 8 + 5 = 23\)
Vậy lớp 10E có 23 bạn chơi ít nhất 1 trong hai môn thể thao trên
b) Tập hợp số học sinh của lớp 10E là \(n\left( {A \cap B} \right) + n\left( {A\backslash B} \right) + n\left( {B\backslash A} \right) + n\left( C \right) = 10 + 8 + 5 + 12 = 35\)
Vậy lớp 10E có tổng 35 học sinh
Bài 8 trang 17 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử, tập con, tập hợp rỗng, và các phép toán hợp, giao, hiệu, bù để giải quyết các bài toán cụ thể.
Bài 8 bao gồm một số câu hỏi và bài tập khác nhau, tập trung vào việc:
Để xác định một tập hợp A có phải là tập hợp con của tập hợp B hay không, ta cần kiểm tra xem mọi phần tử của A đều thuộc B hay không. Nếu điều này đúng, thì A là tập hợp con của B, ký hiệu là A ⊆ B.
Ví dụ: Cho A = {1, 2} và B = {1, 2, 3}. Vì mọi phần tử của A đều thuộc B, nên A ⊆ B.
Phép hợp của hai tập hợp A và B, ký hiệu là A ∪ B, là tập hợp chứa tất cả các phần tử thuộc A hoặc thuộc B (hoặc cả hai). Các phần tử được liệt kê một lần duy nhất.
Ví dụ: Cho A = {1, 2, 3} và B = {3, 4, 5}. A ∪ B = {1, 2, 3, 4, 5}.
Phép giao của hai tập hợp A và B, ký hiệu là A ∩ B, là tập hợp chứa tất cả các phần tử thuộc cả A và B.
Ví dụ: Cho A = {1, 2, 3} và B = {2, 3, 4}. A ∩ B = {2, 3}.
Phép hiệu của hai tập hợp A và B, ký hiệu là A \ B, là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B.
Ví dụ: Cho A = {1, 2, 3} và B = {2, 4}. A \ B = {1, 3}.
Phép bù của tập hợp A trong tập hợp vũ trụ U, ký hiệu là A', là tập hợp chứa tất cả các phần tử thuộc U nhưng không thuộc A.
Ví dụ: Cho U = {1, 2, 3, 4, 5} và A = {1, 3, 5}. A' = {2, 4}.
Ngoài các bài tập cơ bản về các phép toán trên tập hợp, bài 8 còn có thể xuất hiện các dạng bài tập phức tạp hơn, yêu cầu học sinh phải kết hợp nhiều kiến thức và kỹ năng khác nhau. Một số dạng bài tập thường gặp bao gồm:
Để giải bài tập về tập hợp một cách hiệu quả, bạn cần lưu ý một số điều sau:
Bài 8 trang 17 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng rằng với hướng dẫn chi tiết và các lưu ý trên, bạn sẽ tự tin hơn trong việc giải quyết các bài tập liên quan đến chủ đề này.