Bài 12 trang 15 SBT Toán 10 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, phép toán vectơ để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 15 SBT Toán 10 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.
Đề bài
Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.
a) Chọn trục hoành là đường thẳng nối hai chân cổng, gốc tọa độ tại một chân cổng, chân cổng còn lại có hoành độ dương, đơn vị là 1 m. Hãy viết phương trình của vòm cổng.
b) Người ta cần chuyền một thùng hàng hình hộp chữ nhật với chiều cao 3 m. Chiều rộng của thùng hàng tối đa là bao nhiêu để thùng có thể chuyển lọt qua được cổng?
Lưu ý: Đáp số làm tròn đến hàng phần trăm
Lời giải chi tiết
a) Giả sử phương trình mô tả cổng có dạng \(y = a{x^2} + bx + c\)
Từ cách đặt hệ trục ta có:
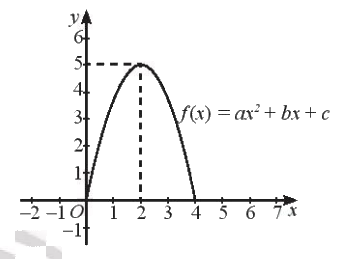
+) Gốc tọa độ tại chân cổng nên \(0 = a{.0^2} + b.0 + c \Leftrightarrow c = 0\)
+) Chân cổng còn lại có hoành độ bằng khoảng cách 2 chân cổng là 4 m nên \(0 = a{.4^2} + b.4 + c \Leftrightarrow 16a + 4b + c = 0\)
+) Đỉnh cổng có tọa độ (2;5) nên \(5 = a{.2^2} + b.2 + c \Leftrightarrow 4a + 2b + c = 5\)
Giải hệ phương trình lập được từ ba phương trình trên ta được \(a = - \frac{5}{4};b = 5;c = 0\)
Vậy phương trình vòm cổng là \(y = - \frac{5}{4}{x^2} + 5x\)
b) Yêu cầu bài toán tương đương với tìm các giá trị của x để \(y \ge 3\)
\( \Leftrightarrow - \frac{5}{4}{x^2} + 5x \ge 3 \Leftrightarrow - \frac{5}{4}{x^2} + 5x - 3 \ge 0 \Leftrightarrow \frac{{10 - 2\sqrt {10} }}{5}x \le \frac{{10 + 2\sqrt {10} }}{5}\)
Suy ra chiều rộng tối đa mà thùng hàng có thể qua cổng là \(\frac{{10 + 2\sqrt {10} }}{5} - \frac{{10 - 2\sqrt {10} }}{5} = \frac{{4\sqrt {10} }}{5} \approx 2,53\)
Vậy chiều rộng tối ra của thùng hàng gần bằng 2,53 m
Bài 12 trang 15 SBT Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 12 trang 15 SBT Toán 10 Chân trời sáng tạo thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập và đưa ra lời giải chi tiết.
Trước khi bắt đầu giải bài tập, chúng ta cần ôn lại một số lý thuyết quan trọng. Ví dụ, nếu bài tập yêu cầu tính tích vô hướng của hai vectơ a và b, chúng ta cần nhớ công thức:
a.b = |a||b|cos(θ)
Trong đó, θ là góc giữa hai vectơ a và b.
Sau khi nắm vững lý thuyết, chúng ta cần đọc kỹ đề bài và phân tích xem bài toán yêu cầu gì. Xác định các vectơ đã cho, các thông tin liên quan và mục tiêu cần đạt được.
Dưới đây là ví dụ về lời giải chi tiết một bài tập tương tự:
Bài tập: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính tích vô hướng của hai vectơ này.
Lời giải:
Tích vô hướng của hai vectơ a và b được tính như sau:
a.b = (1)(-3) + (2)(4) = -3 + 8 = 5
Vậy, tích vô hướng của hai vectơ a và b là 5.
Để giải nhanh các bài tập về vectơ, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức, các em có thể tự giải thêm một số bài tập tương tự. Dưới đây là một số gợi ý:
Bài 12 trang 15 SBT Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp các em học sinh rèn luyện kỹ năng giải toán về vectơ. Hy vọng với lời giải chi tiết và các mẹo giải nhanh mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.