Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 5 trang 13 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
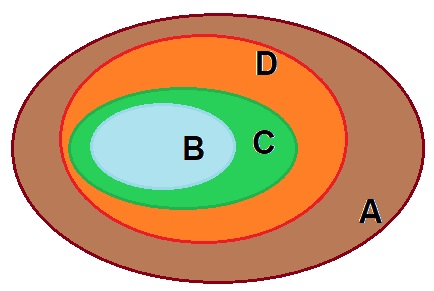
Hãy chỉ ra các quan hệ bao hàm giữa các tập hợp sau và vẽ đồ thị Ven dể biểu diễn các quan hệ đó
Đề bài
Hãy chỉ ra các quan hệ bao hàm giữa các tập hợp sau và vẽ đồ thị Ven dể biểu diễn các quan hệ đó
a) A = {x | x là tứ giác}
b) B = {x | x là hình vuông}
c) C = {x | x là hình chữ nhật}
d) D = {x | x là hình bình hành}
Phương pháp giải - Xem chi tiết
Hai tập hợp A và B được gọi là quan hệ bao hàm nếu \(A \subset B\) hoặc \(B \supset A\)
Lời giải chi tiết
Mỗi hình vuông, hình chữ nhật và hình bình hành đều là tứ giác nên \(B,C,D \subset A\)
Mỗi hình vuông và hình chữ nhật đều là hình bình hành nên \(B,C \subset D\)
Mỗi hình vuông đều là hình chữ nhật nên \(B \subset C\)
Ta có đồ thị Ven biểu diễn mỗi quan hệ bao hàm trên như hình dưới đây
Bài 5 trang 13 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử của tập hợp, tập con, tập hợp rỗng, và các phép toán hợp, giao, hiệu, bù để giải quyết các bài toán cụ thể.
Bài 5 bao gồm một số câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Để giải bài 5 trang 13 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ 1: Cho tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm:
Giải:
Khi thực hiện các phép toán trên tập hợp, cần chú ý đến thứ tự thực hiện các phép toán và sử dụng đúng các ký hiệu toán học. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, học sinh có thể tự giải các bài tập sau:
Bài 5 trang 13 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tập hợp và các phép toán trên tập hợp. Bằng cách nắm vững kiến thức lý thuyết và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán liên quan đến tập hợp một cách hiệu quả.
| Phép toán | Ký hiệu | Định nghĩa |
|---|---|---|
| Hợp | ∪ | Tập hợp chứa tất cả các phần tử thuộc A hoặc B (hoặc cả hai). |
| Giao | ∩ | Tập hợp chứa tất cả các phần tử thuộc cả A và B. |
| Hiệu | \ | Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. |
| Phần bù | c | Tập hợp chứa tất cả các phần tử không thuộc A (trong một tập hợp vũ trụ cho trước). |