Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 75 sách bài tập Toán 10 Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
a) Tính diện tích tam giác ABC b) Tính bán kính đường tròn nội tiếp của tam giác ABC
Đề bài
Cho tam giác ABC có \(a = 24\)cm, \(b = 26\)cm, \(c = 30\)cm
a) Tính diện tích tam giác ABC
b) Tính bán kính đường tròn nội tiếp của tam giác ABC
Lời giải chi tiết
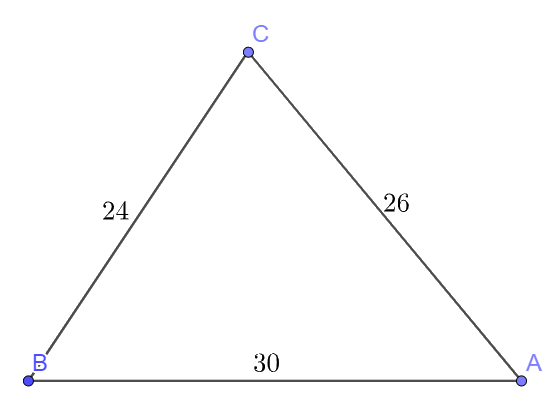
a) Ta có: \(p = \frac{1}{2}\left( {24 + 26 + 30} \right) = 40\) (cm)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {40.\left( {40 - 24} \right)\left( {40 - 26} \right)\left( {40 - 30} \right)} = 80\sqrt {14} \) (cm2)
b) Ta có công thức \(S = pr\)
Suy ra \(r = \frac{S}{p} = \frac{{80\sqrt {14} }}{{40}} = 2\sqrt {14} \) (cm)
Bài 6 trang 75 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 75 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Ví dụ 1: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b.
Giải:a + b = (1 + (-3); 2 + 4) = (-2; 6).
Ví dụ 2: Chứng minh rằng a - (b - c) = a - b + c.
Giải: Ta có a - (b - c) = a - b + c (theo tính chất phân phối của phép trừ đối với phép cộng).
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán 10 để được hướng dẫn chi tiết hơn.
Vectơ là một khái niệm quan trọng trong Toán học, đặc biệt là trong hình học và vật lý. Việc nắm vững kiến thức về vectơ sẽ giúp bạn giải quyết các bài toán phức tạp một cách dễ dàng hơn, đồng thời mở ra cánh cửa cho việc học các môn khoa học khác.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 6 trang 75 sách bài tập Toán 10 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!