Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 102 sách bài tập Toán 10 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ
Đề bài
Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
a) cùng hướng? b) ngược hướng?
Lời giải chi tiết
a) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng
=> A, B, C thẳng hàng và B, C nằm về cùng phía so với điểm A.
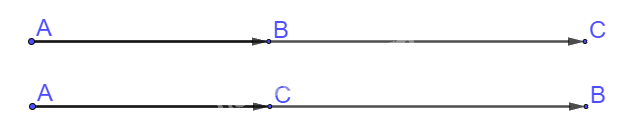
b) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) ngược hướng
=> A, B, C thẳng hàng và B, C nằm về hai phía so với điểm A.
(Hay A, B, C thẳng hàng và A nằm giữa B và C)
Bài 1 trang 102 sách bài tập Toán 10 - Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ, và các ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa vectơ, các phép cộng, trừ, nhân vectơ với một số thực, và cách biểu diễn vectơ trong hệ tọa độ.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 1 trang 102, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài tập. Dưới đây là ví dụ về lời giải cho một số câu hỏi thường gặp:
Lời giải: Vectơ AB được xác định bằng hiệu tọa độ của điểm B trừ đi tọa độ của điểm A. Nếu A(xA, yA) và B(xB, yB) thì AB = (xB - xA, yB - yA).
Lời giải: Để tính tổng hai vectơ, ta cộng các thành phần tương ứng của chúng. a + b = (1 + 3, 2 + 4) = (4, 6).
Để học tập hiệu quả hơn, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn đã có thể tự tin giải bài 1 trang 102 sách bài tập Toán 10 - Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong học tập.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định vectơ | Sử dụng định nghĩa vectơ và hiệu tọa độ. |
| Phép toán vectơ | Thực hiện các phép cộng, trừ, nhân vectơ theo quy tắc. |
| Chứng minh đẳng thức vectơ | Biến đổi các vế của đẳng thức để chúng tương đương nhau. |