Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 27 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để nắm vững kiến thức Toán 10 nhé!
Cho bất phương trình bậc nhất hai ẩn: 2x - 5y + 10 > 0
Đề bài
Cho bất phương trình bậc nhất hai ẩn: \(2x - 5y + 10 > 0\)
a) Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng Oxy
b) \(\left( {1;3} \right)\) có phải là nghiệm của bất phương trình trên không?
c) Chỉ ra 2 cặp số thỏa mãn bất phương trình trên
Phương pháp giải - Xem chi tiết
a) Bước 1: Vẽ đường thẳng của phương trình \(2x - 5y + 10 = 0\)
Bước 2: Xét 1 điểm bất kỳ thay vào bất phương trình và kết luận
b) Thay tọa độ điểm \(\left( {1;3} \right)\) vào bất phương trình và kiểm tra
c) Chọn x (hoặc y) bất kỳ và tìm ẩn còn lại thỏa mãn
Lời giải chi tiết
a) Vẽ đường thẳng \(d:2x - 5y + 10 = 0\) đi qua hai điểm \(A\left( {0;2} \right)\) và \(B\left( { - 5;0} \right)\)
Xét gốc tọa độ \(O\left( {0;0} \right)\)
Ta thấy \(O \notin d\) và \(2.0 - 5.0 + 10 = 10 > 0\). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ d, chứa gốc tọa độ O (miền không gạch chéo như hình dưới)
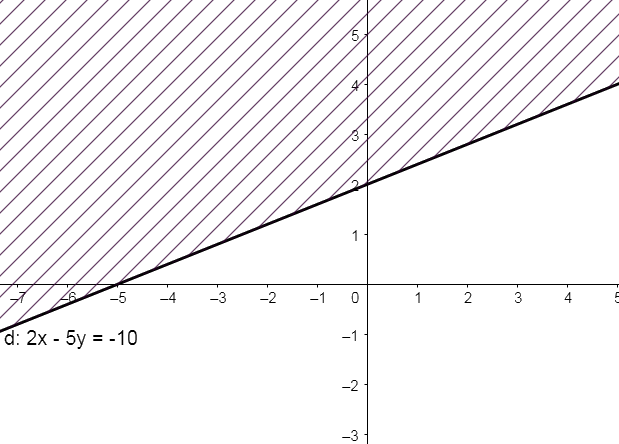
b) Thay tọa độ điểm \(\left( {1;3} \right)\) vào bất phương trình trên ta có:
\(2.1 - 5.3 + 10 = - 3 < 0\). Do đó \(\left( {1;3} \right)\) không là nghiệm của bất phương trình đã cho
c) Chọn \(x = 0 \Rightarrow 2.0 - 5y + 10 > 0 \Rightarrow y < 2\)
Vậy 2 cặp số thỏa mãn là nghiệm của bất phương trình đã cho là \(\left( {0;0} \right)\) và \(\left( {0;1} \right)\)
Bài 1 trang 27 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử của tập hợp, tập con, tập rỗng, và các phép toán hợp, giao, hiệu của hai tập hợp để giải quyết các bài toán cụ thể.
Bài 1 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải quyết bài 1 trang 27 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 1 trang 27 sách bài tập Toán 10 Chân trời sáng tạo:
Đề bài: Liệt kê các phần tử của tập hợp A = {x | x là số tự nhiên nhỏ hơn 10}.
Lời giải: Tập hợp A bao gồm các số tự nhiên nhỏ hơn 10, tức là A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Đề bài: Xác định xem tập hợp B = {1, 2, 3} có phải là tập con của tập hợp C = {1, 2, 3, 4, 5} hay không.
Lời giải: Vì tất cả các phần tử của tập hợp B đều thuộc tập hợp C, nên B là tập con của C. Ký hiệu: B ⊂ C.
Đề bài: Cho hai tập hợp D = {1, 2, 3, 4} và E = {3, 4, 5, 6}. Tìm tập hợp D ∪ E (hợp của D và E).
Lời giải: Tập hợp D ∪ E bao gồm tất cả các phần tử thuộc D hoặc E (hoặc cả hai). Do đó, D ∪ E = {1, 2, 3, 4, 5, 6}.
Đề bài: Cho hai tập hợp D = {1, 2, 3, 4} và E = {3, 4, 5, 6}. Tìm tập hợp D ∩ E (giao của D và E).
Lời giải: Tập hợp D ∩ E bao gồm các phần tử thuộc cả D và E. Do đó, D ∩ E = {3, 4}.
Đề bài: Cho hai tập hợp D = {1, 2, 3, 4} và E = {3, 4, 5, 6}. Tìm tập hợp D \ E (hiệu của D và E).
Lời giải: Tập hợp D \ E bao gồm các phần tử thuộc D nhưng không thuộc E. Do đó, D \ E = {1, 2}.
Bài 1 trang 27 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập cơ bản giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.