Giải bài 8 trang 80 Sách bài tập Toán 10 - Chân trời sáng tạo

Giải bài 8 trang 80 sách bài tập toán 10 - Chân trời sáng tạo

Giải bài 8 trang 80 Sách bài tập Toán 10 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 80 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.

Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn dễ dàng theo dõi và hiểu bài.

Diện tích của tam giác GFC là

Đề bài

Cho tam giác ABC vuông cân tại A có \(AB = AC = 30\) cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích của tam giác GFC là:

A. 50 \(cm^2\)

B. \(50\sqrt 2 \) \(cm^2\)

C. 75 \(cm^2\)

D.\(15\sqrt {105} \) \(cm^2\)

Lời giải chi tiết

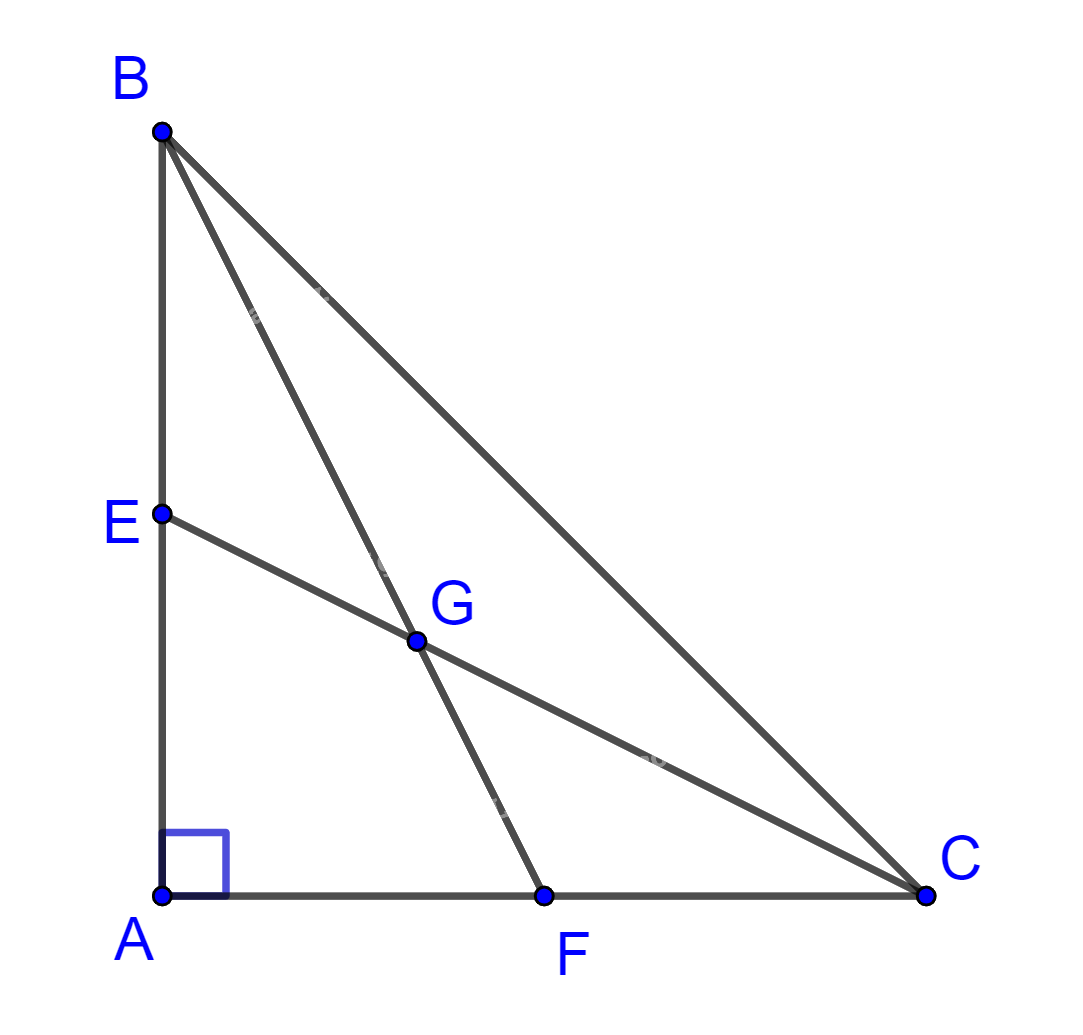
Giải bài 8 trang 80 sách bài tập toán 10 - Chân trời sáng tạo 1

Ta có CE, BF là đường trung tuyến nên G là trọng tâm của tam giác ABC.

\( \Rightarrow GF = \frac{1}{3}BF \Rightarrow {S_{\Delta GCF}} = \frac{1}{3}{S_{\Delta BCF}}\)

Mà \(CF = \frac{1}{2}AC \Rightarrow {S_{\Delta BCF}} = \frac{1}{2}{S_{\Delta ABC}}\)

\( \Rightarrow {S_{\Delta GCF}} = \frac{1}{6}{S_{\Delta ABC}} = \frac{1}{6}.\frac{1}{2}.30.30 = 75\left( {c{m^2}} \right)\)

Chọn C

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 8 trang 80 sách bài tập toán 10 - Chân trời sáng tạo đặc sắc thuộc chuyên mục giải bài tập toán 10 trên nền tảng toán học. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 8 trang 80 Sách bài tập Toán 10 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Bài 8 trang 80 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về hàm số bậc hai. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:

Định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax² + bx + c, với a ≠ 0.
Đồ thị hàm số bậc hai (Parabol): Đồ thị của hàm số bậc hai là một parabol có đỉnh I(x₀; y₀), trục đối xứng x = x₀.
Các yếu tố của parabol: Đỉnh, trục đối xứng, điểm đối xứng qua trục tung, giao điểm với trục hoành (nghiệm của phương trình bậc hai).
Các dạng phương trình bậc hai: Phương trình bậc hai có các dạng khác nhau như phương trình tổng quát, phương trình thiếu, phương trình hoàn chỉnh.

Nội dung bài 8 trang 80 sách bài tập Toán 10 Chân trời sáng tạo thường bao gồm các dạng bài tập sau:

Xác định các hệ số a, b, c của hàm số bậc hai.
Tìm tọa độ đỉnh của parabol.
Xác định trục đối xứng của parabol.
Vẽ đồ thị hàm số bậc hai.
Giải phương trình bậc hai.
Tìm điều kiện để phương trình bậc hai có nghiệm.
Ứng dụng hàm số bậc hai vào giải quyết các bài toán thực tế.

Hướng dẫn giải chi tiết bài 8 trang 80

Để giúp bạn hiểu rõ hơn về cách giải bài 8 trang 80, chúng ta sẽ đi vào giải chi tiết từng câu hỏi. (Lưu ý: Vì bài tập cụ thể không được cung cấp, phần này sẽ trình bày cách tiếp cận chung và ví dụ minh họa.)

Ví dụ minh họa:

Bài tập: Cho hàm số y = 2x² - 4x + 1. Hãy tìm tọa độ đỉnh của parabol.

Giải:

Xác định hệ số a, b, c: a = 2, b = -4, c = 1.
Tính hoành độ đỉnh: x₀ = -b / (2a) = -(-4) / (2 * 2) = 1.
Tính tung độ đỉnh: y₀ = a * x₀² + b * x₀ + c = 2 * 1² - 4 * 1 + 1 = -1.
Kết luận: Tọa độ đỉnh của parabol là I(1; -1).

Các lưu ý khi giải bài tập về hàm số bậc hai

Nắm vững các công thức: Các công thức tính đỉnh, trục đối xứng, nghiệm của phương trình bậc hai là rất quan trọng.
Phân tích kỹ đề bài: Đọc kỹ đề bài để xác định đúng yêu cầu và các thông tin đã cho.
Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn khi giải bài 8 trang 80 sách bài tập Toán 10 Chân trời sáng tạo và đạt kết quả tốt nhất trong học tập. Chúc bạn thành công!