Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 34 sách bài tập Toán 10 Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
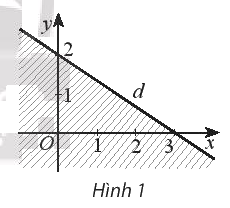
Miền không gạch chéo (không kể bờ d) trong hình 11 là miền nghiệm của bất phương trình nào trong các bất phương trình sau đây:
Đề bài
Miền không gạch chéo (không kể bờ d) trong hình 11 là miền nghiệm của bất phương trình nào trong các bất phương trình sau đây:
A. \(2x + 3y < 6\)
B. \(2x + 3y > 6\)
C. \(\frac{x}{2} + \frac{y}{3} > 0\)
D. \(\frac{x}{2} + \frac{y}{3} < 1\)
Lời giải chi tiết
Dễ thấy gốc tọa độ (0; 0) không thuộc miền nghiệm => Loại A, D.
Điểm (1;0) không thuộc miền nghiệm => Loại C
Chọn B.
Bài 3 trang 34 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các khái niệm như tập hợp, phần tử của tập hợp, tập con, tập rỗng, và các phép toán hợp, giao, hiệu, bù để giải quyết các bài toán cụ thể.
Bài 3 thường bao gồm các dạng bài tập sau:
Để xác định các tập hợp, bạn cần nắm vững định nghĩa của các khái niệm liên quan đến tập hợp. Ví dụ:
Khi gặp bài toán yêu cầu xác định tập hợp, bạn cần liệt kê tất cả các phần tử thỏa mãn điều kiện đề bài.
Để thực hiện các phép toán trên tập hợp, bạn cần nắm vững định nghĩa của từng phép toán:
Khi thực hiện các phép toán, bạn cần cẩn thận để tránh bỏ sót hoặc lặp lại phần tử.
Khi giải các bài toán ứng dụng, bạn cần phân tích đề bài để xác định các tập hợp liên quan và các phép toán cần thực hiện. Sau đó, bạn áp dụng kiến thức về tập hợp để giải quyết bài toán.
Ví dụ: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tính A ∪ B, A ∩ B, A \ B, CAB.
Giải:
Bài 3 trang 34 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.