Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 trang 33 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất cho học sinh, sinh viên. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này ngay nhé!
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau đây:
Đề bài
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau đây:
a) \(\left\{ \begin{array}{l}x + y - 4 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x + 2y - 5 < 0\\0 \le x \le 3\\y \ge 0\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn miền nghiệm của từng bất phương trình trong hệ
Bước 2: Kết hợp miền nghiệm của các bất phương trình và kết luận
Lời giải chi tiết
a) Biểu diễn miền nghiệm của mỗi bất phương trình có trong hệ trên mặt phẳng Oxy, ta được như hình dưới
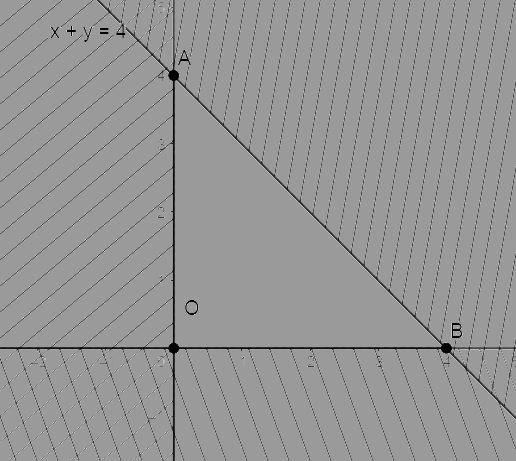
Miền không gạch chéo (kể cả bờ là các đoạn thẳng OA, OB và AB) là phần giao của ba miền nghiệm của ba bất phương trình và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho
b) Hệ đã cho được viết lại thành \(\left\{ \begin{array}{l}x + 2y - 5 < 0\\x \ge 0\\x \le 3\\y \ge 0\end{array} \right.\)
Biểu diễn miền nghiệm của mỗi bất phương trình có trong hệ trên mặt phẳng Oxy, ta được như hình dưới
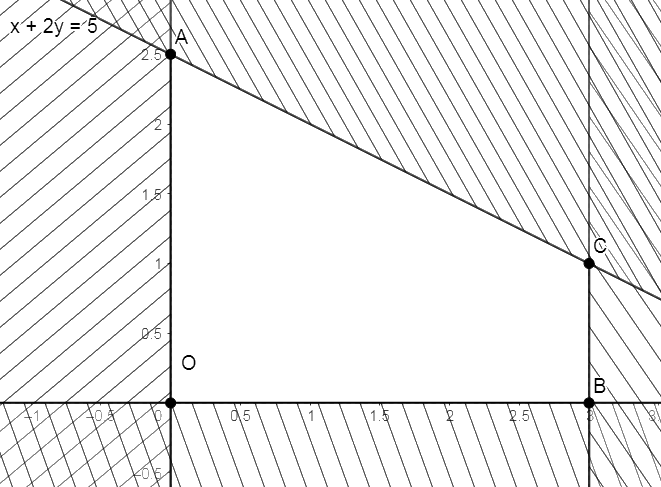
Miền không gạch chéo (kể cả bờ là các đoạn thẳng OA, OB và BC ) của ba bất phương trình dưới và không tính bờ là đoạn thẳng AC của bất phương trình thứ nhất là phần giao của bốn miền nghiệm của bốn bất phương trình và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho
Bài 1 trang 33 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp. Bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa, ký hiệu, và các quy tắc liên quan đến tập hợp để có thể giải quyết một cách chính xác.
Bài 1 trang 33 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Cho tập hợp A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm tập hợp A ∪ B.
Lời giải:
A ∪ B = {1, 2, 3, 4, 5, 6, 7}
Cho tập hợp A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm tập hợp A ∩ B.
Lời giải:
A ∩ B = {3, 4, 5}
Cho tập hợp A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm tập hợp A \ B.
Lời giải:
A \ B = {1, 2}
Để giải quyết các bài tập về tập hợp một cách hiệu quả, các em học sinh cần lưu ý những điều sau:
Kiến thức về tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
Bài 1 trang 33 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tập hợp. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài tập tương tự.