Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 79 sách bài tập Toán 10 Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và kèm theo các giải thích chi tiết để bạn có thể nắm vững kiến thức.
Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ Chí Minh và Cần Thơ.
Đề bài
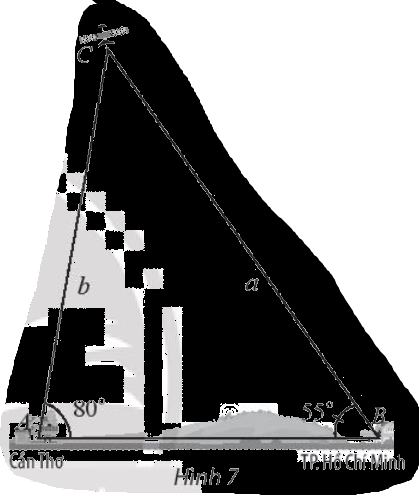
Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ Chí Minh và Cần Thơ. Khi vệ tinh nằm giữa hai trạm này, góc nâng của nó được quan sát đồng thời là \(55^\circ \)tại thành phố Hồ Chí Minh và \(80^\circ \) tại Cần Thơ. Hỏi khi đó vệ tinh cách trạm quan sát tại Cần Thơ bao xa? Biết rằng, khoảng cách giữa hai trạm quan sát là 127 km.
Phương pháp giải - Xem chi tiết
Bước 1: Tính góc C
Bước 2: Áp dụng định lí sin
Lời giải chi tiết
Ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {80^\circ + 55^\circ } \right) = 45^\circ \)
Sử dụng định lí sin ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{127}}{{\sin 45^\circ }} \Rightarrow AC = \frac{{127}}{{\sin 45^\circ }}.\sin 55^\circ \simeq 147,124\) km
Vậy khi đó vệ tinh cách trạm quan sát tại Cần Thơ xấp xỉ 147,124 km
Bài 4 trang 79 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng và các điểm đặc biệt của parabol để giải quyết các bài toán thực tế.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 4. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một ví dụ minh họa:
Cho hàm số y = x2 - 4x + 3. Hãy tìm:
Lời giải:
Khi giải bài tập về hàm số bậc hai, bạn cần chú ý:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 10 Chân trời sáng tạo hoặc trên các trang web học toán online.
Bài 4 trang 79 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp bạn hiểu sâu hơn về hàm số bậc hai. Hy vọng với lời giải chi tiết và các phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn khi giải các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| xđỉnh = -b/(2a) | Tính hoành độ đỉnh của parabol |
| yđỉnh = -Δ/(4a) | Tính tung độ đỉnh của parabol |
| x = -b/(2a) | Phương trình trục đối xứng của parabol |