Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 3 trang 79 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn dễ dàng theo dõi và hiểu bài.
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng
Đề bài
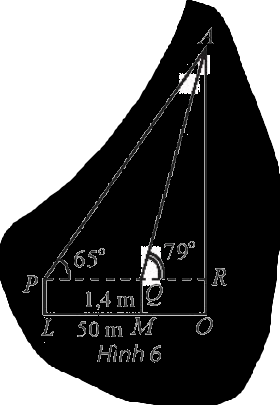
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {RQA} = 79^\circ \), người đó lùi ra xa một khoảng cách \(LM = 50\) m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {RPA} = 65^\circ \). Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là \(PL = QM = 1,4\) m (hình 6)
Lời giải chi tiết
Ta có chiều cao của nhà cao tầng là \(AO = AR + RO = AR + 1,4\)
Góc \(\widehat {AQR}\) là góc ngoài của tam giác APQ tại đỉnh Q suy ra \(\widehat {AQR} = \widehat {APQ} + \widehat {QAP} \Rightarrow \widehat {QAP} = \widehat {AQR} - \widehat {APQ} = 79^\circ - 65^\circ = 14^\circ \)
Áp dụng định lí sin vào tam giác APQ ta có:
\(\frac{{PQ}}{{\sin \widehat {PAQ}}} = \frac{{AQ}}{{\sin \widehat {APQ}}} = \frac{{50}}{{\sin 14^\circ }} \Rightarrow AQ = \frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ \)
Xét tam giác AQR ta có:
\(\frac{{AR}}{{\sin \widehat {AQR}}} = \frac{{AQ}}{{\sin \widehat {ARQ}}} = \frac{{\frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ }}{{\sin 90^\circ }} \Rightarrow AR = \frac{{\frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ }}{{\sin 90^\circ }}.\sin 79^\circ \simeq 183,87\)
\( \Rightarrow AO \simeq 183,87 + 1,4 = 185,27\)
Vậy tòa nhà cao xấp xỉ 185,27 m
Bài 3 trang 79 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về hàm số bậc hai. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Nội dung bài 3 trang 79 sách bài tập Toán 10 Chân trời sáng tạo:
Bài 3 yêu cầu chúng ta tìm tập xác định của hàm số. Để làm được điều này, chúng ta cần xác định điều kiện để hàm số có nghĩa. Thông thường, điều kiện để hàm số có nghĩa là mẫu số khác 0 và biểu thức dưới dấu căn bậc chẵn lớn hơn hoặc bằng 0.
Hướng dẫn giải chi tiết bài 3 trang 79:
Để giải bài 3 trang 79, chúng ta sẽ tiến hành theo các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm tập xác định là y = √(x - 2). Điều kiện để hàm số có nghĩa là x - 2 ≥ 0, suy ra x ≥ 2. Vậy tập xác định của hàm số là [2, +∞).
Các dạng bài tập tương tự:
Ngoài bài 3 trang 79, sách bài tập Toán 10 Chân trời sáng tạo còn có nhiều bài tập tương tự về tập xác định của hàm số. Để luyện tập và nâng cao kỹ năng giải toán, bạn có thể tham khảo các bài tập sau:
Lưu ý khi giải bài tập về tập xác định:
Ứng dụng của kiến thức về tập xác định:
Kiến thức về tập xác định có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học, đặc biệt là trong việc nghiên cứu hàm số và giải phương trình. Việc nắm vững kiến thức này sẽ giúp bạn hiểu sâu hơn về các khái niệm toán học và giải quyết các bài toán phức tạp một cách hiệu quả.
Tổng kết:
Bài 3 trang 79 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về tập xác định của hàm số. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, bạn sẽ tự tin hơn trong quá trình học tập và giải toán.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức. Chúc bạn học tập tốt!