Bài 5 trang 55 sách bài tập Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để bạn có thể nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm khoảng biến thiên và tập giá trị của các hàm số sau:
Đề bài
Tìm khoảng biến thiên và tập giá trị của các hàm số sau:
a) \(y = f\left( x \right) = - 2{x^2} - 4x + 7\)
b) \(y = f\left( x \right) = {x^2} - 6x + 1\)
Lời giải chi tiết
a) Hàm số \(y = f\left( x \right) = - 2{x^2} - 4x + 7\) có \(a = - 2 < 0\) và tọa độ đỉnh gồm \({x_S} = - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.\left( { - 2} \right)}} = - 1,{y_S} = - 2.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 7 = 9\)
Ta có bảng biến thiên sau
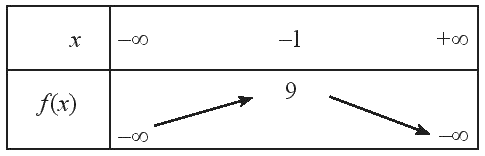
Vậy hàm số đồng biến trên \(\left( { - \infty ;-1} \right)\) và nghịch biến \(\left( -1; + \infty \right)\)
Hàm số có tập giá trị \(T = \left( { - \infty ; 9} \right]\)
b) Hàm số \(y = f\left( x \right) = {x^2} - 6x + 1\) có \(a = 1> 0\) và tọa độ đỉnh gồm \({x_S} = - \frac{b}{{2a}} = - \frac{{ -6}}{{2.1}} = 3,{y_S} = {3^2} - 6.3 + 1 = -8\)
Ta có bảng biến thiên sau
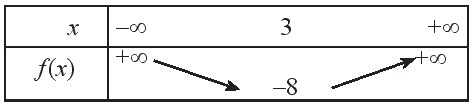
Vậy hàm số nghịch biến trên \(\left( { - \infty ;3} \right)\) và đồng biến \(\left( 3; + \infty \right)\)
Hàm số có tập giá trị \(T = \left( {-8; + \infty } \right]\)
Bài 5 trang 55 sách bài tập Toán 10 Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về vectơ, phép cộng, trừ vectơ, phép nhân vectơ với một số thực để giải quyết các bài toán cụ thể. Việc hiểu rõ các định nghĩa, tính chất và quy tắc là nền tảng để tiếp cận bài toán một cách hiệu quả.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức cơ bản:
Để giải bài 5 trang 55, chúng ta cần phân tích đề bài, xác định các vectơ liên quan và áp dụng các phép toán vectơ phù hợp. Dưới đây là hướng dẫn chi tiết cho từng ý của bài tập:
(Nội dung ý a của bài tập, ví dụ: Cho hình bình hành ABCD, tìm vectơ AB + AD)
Giải: Theo quy tắc hình bình hành, AB + AD = AC. Do đó, vectơ AB + AD bằng vectơ AC.
(Nội dung ý b của bài tập, ví dụ: Cho hai vectơ a và b, tìm vectơ 2a - b)
Giải: Vectơ 2a có cùng hướng và độ dài gấp đôi vectơ a. Vectơ -b có cùng hướng ngược với vectơ b và độ dài bằng độ dài của vectơ b. Do đó, vectơ 2a - b là vectơ có hướng và độ dài được xác định bởi phép trừ vectơ.
(Nội dung ý c của bài tập, ví dụ: Chứng minh rằng nếu AB = CD thì AC = BD)
Giải: Nếu AB = CD, thì hai vectơ này có cùng độ dài và cùng hướng. Do đó, AB - CD = 0. Từ đó suy ra AC = BD.
Để củng cố kiến thức, bạn có thể giải thêm các bài tập tương tự sau:
Khi giải các bài tập về vectơ, bạn cần lưu ý những điều sau:
Vectơ có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ cách giải bài 5 trang 55 sách bài tập Toán 10 Chân trời sáng tạo. Chúc bạn học tập tốt!