Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 36 sách bài tập Toán 10 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn dễ dàng theo dõi và hiểu bài.
Một học sinh dự dịnh làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm một bình hoa loại nhỏ và sẽ bán được 100 nghìn đồng,
Đề bài
Một học sinh dự dịnh làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm một bình hoa loại nhỏ và sẽ bán được 100 nghìn đồng, 90 phút để làm một bình hoa loại lớn và sẽ bán được 200 nghìn đồng. Học sinh này chỉ thu xếp được 15 giờ nghỉ để làm và ban tổ chức yêu cầu phải làm ít nhất 12 bình hoa. Hãy chi biết bạn ấy cần làm bao nhiêu bình hoa mỗi loại để gây quỹ được nhiều nhất.
Lời giải chi tiết
Đổi 90 phút = 1,5 giờ
Gọi x, y lần lượt là số lượng bình hoa loại nhỏ và loại lớn ta có hệ bất phương trình miêu tả diều kiện ràng buộc đối với x, y như sau:
\(\left\{ \begin{array}{l}x + 1,5y \le 15\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.\)
Miền nghiệm của hệ bất phương trình là miền nghiệm tam giác ABC, trong đó \(A(6;6),B(12;0),C(15;0)\)
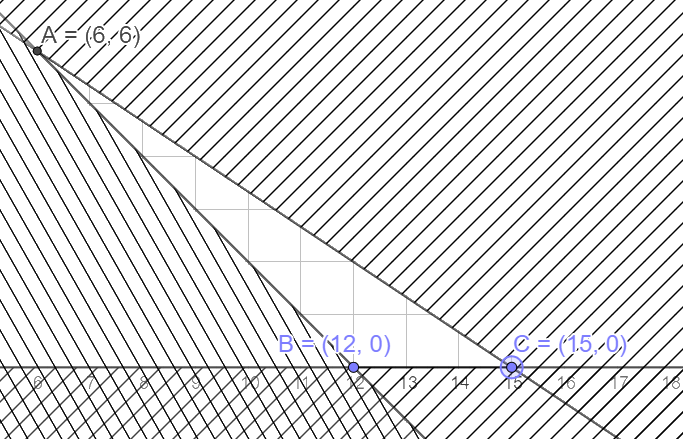
Gọi F là số tiền gây quỹ (đơn vị: nghìn đồng) ta có: \(F = 100x + 200y\)
Tại \(A(6;6)\): \(F = 100.6 + 200.6 = 1800\)
Tại \(B(12;0)\): \(F = 100.6 + 200.6 = 1800\)
Tại \(C(15;0)\): \(F = 100.15 + 200.0 = 1500\)
Ta thấy F đạt GTLN bằng 1800 tại \(A(6;6)\)
Vậy bạn đó nên làm 6 bình hoa nhỏ và 6 bính hoa lớn để số tiền gây quỹ lớn nhất.
Bài 8 trang 36 sách bài tập Toán 10 Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này tập trung vào việc vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán cụ thể.
Bài 8 bao gồm các dạng bài tập sau:
Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b.
Giải:
Để tính tổng của hai vectơ, ta cộng các thành phần tương ứng của chúng:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
Cho vectơ a = (2; -1) và số thực k = 3. Tính ka.
Giải:
Để tính tích của một số với một vectơ, ta nhân số đó với mỗi thành phần của vectơ:
ka = 3(2; -1) = (3 * 2; 3 * (-1)) = (6; -3)
Cho ba điểm A(1; 2), B(3; 4), C(5; 6). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Giải:
Để chứng minh ba điểm A, B, C thẳng hàng, ta có thể chứng minh rằng vectơ AB và AC cùng phương. Tức là, tồn tại một số thực k sao cho AC = kAB.
Tính vectơ AB = (3 - 1; 4 - 2) = (2; 2)
Tính vectơ AC = (5 - 1; 6 - 2) = (4; 4)
Ta thấy AC = 2AB, do đó vectơ AB và AC cùng phương. Vậy ba điểm A, B, C thẳng hàng.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, bạn đã có thể tự tin giải bài 8 trang 36 sách bài tập Toán 10 Chân trời sáng tạo. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tập tốt!