Giải bài 1 trang 65 SGK Toán 8 – Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 65 SGK Toán 8 – Cánh diều. Bài học này thuộc chương trình Toán 8, tập trung vào việc ôn tập và rèn luyện các kiến thức đã học.

Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.

Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn

Đề bài

Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn \(MN//BC\). Chứng minh \(NA = NC\) và \(MN = \frac{1}{2}BC\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài 1 trang 65 SGK Toán 8 – Cánh diều 1

Dựa vào hệ quả của định lý Thales để chứng minh N là trung điểm của AC.

Chứng minh MN là đường trung bình của tam giác ABC để suy ra \(MN = \frac{1}{2}BC\).

Lời giải chi tiết

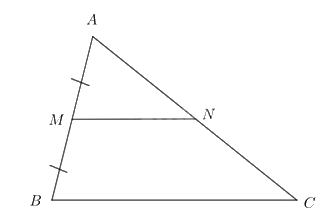
Giải bài 1 trang 65 SGK Toán 8 – Cánh diều 2

Theo đề bài ta có \(MN//BC\) nên \(\frac{AM}{MB} = \frac{AN}{NC}\)

Mà \( AM = MB\)

\(\Rightarrow \frac{AM}{MB} = \frac{AN}{NC} = 1 \Rightarrow AN = NC\)

\(\Rightarrow\) N là trung điểm của AC

Khi đó MN là đường trung bình của tam giác ABC

\( \Rightarrow MN = \frac{1}{2}BC\).

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 1 trang 65 SGK Toán 8 – Cánh diều đặc sắc thuộc chuyên mục toán 8 trên đề thi toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 1 trang 65 SGK Toán 8 – Cánh diều: Tổng quan và Phương pháp giải

Bài 1 trang 65 SGK Toán 8 – Cánh diều là một bài tập ôn tập, giúp học sinh củng cố kiến thức về các dạng toán đã học trong chương trình. Bài tập thường yêu cầu học sinh vận dụng các công thức, định lý và kỹ năng giải toán đã được học để giải quyết các bài toán cụ thể.

Nội dung bài tập

Bài 1 thường bao gồm các dạng bài tập sau:

Bài tập về phân tích đa thức thành nhân tử: Học sinh cần sử dụng các phương pháp như đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm đa thức để phân tích đa thức thành nhân tử.
Bài tập về rút gọn biểu thức: Học sinh cần thực hiện các phép toán cộng, trừ, nhân, chia đa thức để rút gọn biểu thức.
Bài tập về giải phương trình: Học sinh cần sử dụng các phương pháp giải phương trình đã học để tìm nghiệm của phương trình.
Bài tập về ứng dụng thực tế: Học sinh cần vận dụng kiến thức đã học để giải quyết các bài toán liên quan đến thực tế.

Hướng dẫn giải chi tiết bài 1 trang 65 SGK Toán 8 – Cánh diều

Để giải bài 1 trang 65 SGK Toán 8 – Cánh diều một cách hiệu quả, học sinh cần:

Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài tập, xác định các dữ kiện đã cho và những điều cần tìm.
Xác định phương pháp giải: Lựa chọn phương pháp giải phù hợp với từng dạng bài tập.
Thực hiện các bước giải: Thực hiện các bước giải một cách chính xác, rõ ràng.
Kiểm tra lại kết quả: Kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa

Bài tập: Phân tích đa thức sau thành nhân tử: x² - 4x + 4

Giải:

Ta có: x² - 4x + 4 = (x - 2)²

Vậy, đa thức x² - 4x + 4 được phân tích thành nhân tử là (x - 2)².

Các lưu ý khi giải bài tập

Nắm vững các công thức, định lý: Việc nắm vững các công thức, định lý là điều kiện cần thiết để giải bài tập một cách chính xác.
Rèn luyện kỹ năng giải toán: Việc rèn luyện kỹ năng giải toán thường xuyên sẽ giúp học sinh giải quyết các bài tập một cách nhanh chóng và hiệu quả.
Sử dụng các công cụ hỗ trợ: Học sinh có thể sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm giải toán để kiểm tra lại kết quả.

Tài liệu tham khảo

Ngoài SGK Toán 8 – Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 8: Cung cấp các bài tập luyện tập đa dạng, giúp học sinh củng cố kiến thức.
Các trang web học toán online: Cung cấp các bài giảng, bài tập và lời giải chi tiết.
Các video hướng dẫn giải toán: Giúp học sinh hiểu rõ hơn về phương pháp giải bài tập.

Kết luận

Bài 1 trang 65 SGK Toán 8 – Cánh diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và các lưu ý trên, các em học sinh sẽ giải bài tập một cách hiệu quả và đạt kết quả tốt nhất.

Dạng bài tập	Phương pháp giải
Phân tích đa thức thành nhân tử	Đặt nhân tử chung, hằng đẳng thức, nhóm đa thức
Rút gọn biểu thức	Thực hiện các phép toán cộng, trừ, nhân, chia
Giải phương trình	Sử dụng các phương pháp giải phương trình