Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 Cánh diều của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 8, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 trang 76, 77, 78 SGK Toán 8 – Cánh diều là một phần quan trọng trong chương trình học, đòi hỏi các em phải hiểu rõ các khái niệm và vận dụng linh hoạt các công thức đã học.
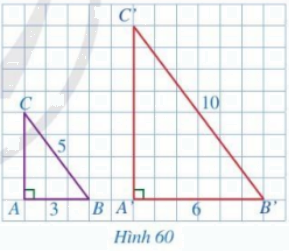
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’
Video hướng dẫn giải
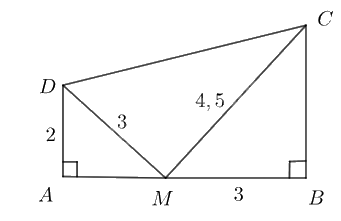
Trong Hình 64, chứng minh tam giác \(CDM\)vuông tại \(M\).
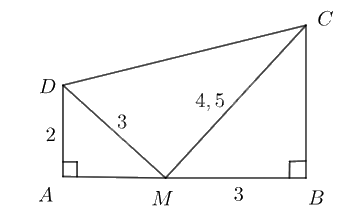
Hình 64
Phương pháp giải:
- Chứng minh \(\Delta ADM \backsim\Delta BMC\)
- Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\)
- Dựa vào tính chất tổng hai góc nhọn trong tam giác vuông bằng \(90^\circ \) ta chứng minh \(\widehat {AMD} + \widehat {BMC} = 90^\circ \)
- Suy ra \(\widehat {DMC} = 90^\circ \) hay tam giác \(CDM\)vuông tại \(M\).
Lời giải chi tiết:
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\)vuông tại \(M\).
Video hướng dẫn giải
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ (Hình 60) sao cho \(AB = 3,\,\,BC = 5,\,\,A'B' = 6,\,\,B'C' = 10\).
a) Tính CA và C’A’
b) So sánh các tỉ số \(\frac{{A'B'}}{{AB}};\,\,\frac{{A'C'}}{{AC}};\,\,\frac{{B'C'}}{{BC}}\)
c) Hai tam giác A’B’C’ và ABC có đồng dạng với nhau hay không?
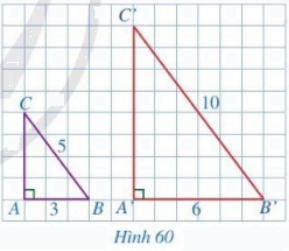
Phương pháp giải:
a) Dựa vào định lý Pytago để tính độ dài CA và C’A’.
b) Tính các tỉ số rồi so sánh.
c) Dựa vào trường hợp đồng dạng thứ nhất của tam giác để xét đồng dạng.
Lời giải chi tiết:
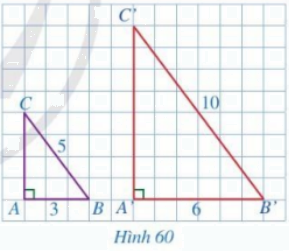
a) Xét tam giác ABC vuông tại A ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {3^2} + C{A^2} = {5^2}\\ \Leftrightarrow C{A^2} = {5^2} - {3^2}\\ \Leftrightarrow C{A^2} = 16\\ \Leftrightarrow CA = 4\end{array}\)
Xét tam giác A’B’C’ vuông tại A’ ta có:
\(A'B{'^2} + A'C{'^2} = B'C{'^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {6^2} + A'C{'^2} = {10^2}\\ \Leftrightarrow A'C{'^2} = {10^2} - {6^2}\\ \Leftrightarrow A'C{'^2} = 64\\ \Leftrightarrow A'C' = 8\end{array}\)
b) Ta có:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{6}{3} = 2\\\frac{{B'C'}}{{BC}} = \frac{{10}}{5} = 2\\\frac{{C'A'}}{{CA}} = \frac{8}{4} = 2\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
c) Xét tam giác A’B’C’ và tam giác ABC có: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
\( \Rightarrow \Delta A'B'C' \backsim\Delta ABC\) (c-c-c)
Video hướng dẫn giải
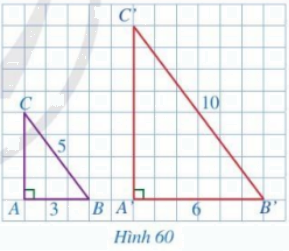
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ (Hình 60) sao cho \(AB = 3,\,\,BC = 5,\,\,A'B' = 6,\,\,B'C' = 10\).
a) Tính CA và C’A’
b) So sánh các tỉ số \(\frac{{A'B'}}{{AB}};\,\,\frac{{A'C'}}{{AC}};\,\,\frac{{B'C'}}{{BC}}\)
c) Hai tam giác A’B’C’ và ABC có đồng dạng với nhau hay không?
Phương pháp giải:
a) Dựa vào định lý Pytago để tính độ dài CA và C’A’.
b) Tính các tỉ số rồi so sánh.
c) Dựa vào trường hợp đồng dạng thứ nhất của tam giác để xét đồng dạng.
Lời giải chi tiết:
a) Xét tam giác ABC vuông tại A ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {3^2} + C{A^2} = {5^2}\\ \Leftrightarrow C{A^2} = {5^2} - {3^2}\\ \Leftrightarrow C{A^2} = 16\\ \Leftrightarrow CA = 4\end{array}\)
Xét tam giác A’B’C’ vuông tại A’ ta có:
\(A'B{'^2} + A'C{'^2} = B'C{'^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {6^2} + A'C{'^2} = {10^2}\\ \Leftrightarrow A'C{'^2} = {10^2} - {6^2}\\ \Leftrightarrow A'C{'^2} = 64\\ \Leftrightarrow A'C' = 8\end{array}\)
b) Ta có:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{6}{3} = 2\\\frac{{B'C'}}{{BC}} = \frac{{10}}{5} = 2\\\frac{{C'A'}}{{CA}} = \frac{8}{4} = 2\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
c) Xét tam giác A’B’C’ và tam giác ABC có: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
\( \Rightarrow \Delta A'B'C' \backsim\Delta ABC\) (c-c-c)
Video hướng dẫn giải
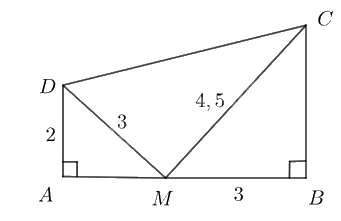
Trong Hình 64, chứng minh tam giác \(CDM\)vuông tại \(M\).
Hình 64
Phương pháp giải:
- Chứng minh \(\Delta ADM \backsim\Delta BMC\)
- Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\)
- Dựa vào tính chất tổng hai góc nhọn trong tam giác vuông bằng \(90^\circ \) ta chứng minh \(\widehat {AMD} + \widehat {BMC} = 90^\circ \)
- Suy ra \(\widehat {DMC} = 90^\circ \) hay tam giác \(CDM\)vuông tại \(M\).
Lời giải chi tiết:
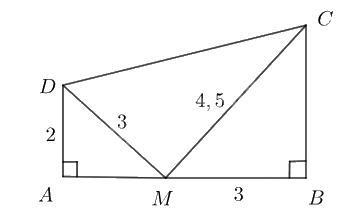
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\)vuông tại \(M\).
Mục 2 của chương trình Toán 8 Cánh diều tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đa thức, đồng thời rèn luyện kỹ năng biến đổi đại số.
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức. Để giải bài tập này, các em cần nắm vững các quy tắc về dấu, bậc của đa thức và các phép toán cơ bản.
Ví dụ:
(2x2 + 3x - 1) + (x2 - 2x + 5) = 3x2 + x + 4
Bài tập này yêu cầu học sinh rút gọn các biểu thức chứa đa thức. Để giải bài tập này, các em cần sử dụng các quy tắc về phân phối, kết hợp và các quy tắc rút gọn khác.
Ví dụ:
2x(x - 3) + 5x2 - 10x = 2x2 - 6x + 5x2 - 10x = 7x2 - 16x
Bài tập này yêu cầu học sinh tìm giá trị của biểu thức khi biết giá trị của biến. Để giải bài tập này, các em cần thay giá trị của biến vào biểu thức và thực hiện các phép tính.
Ví dụ:
Cho x = 2, tìm giá trị của biểu thức 3x2 - 5x + 1. Ta có: 3(2)2 - 5(2) + 1 = 12 - 10 + 1 = 3
Để học tốt môn Toán 8, các em cần có phương pháp học tập khoa học, chăm chỉ luyện tập và luôn tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a + b)(a - b) | Hiệu hai bình phương |
Hy vọng với những giải thích chi tiết và phương pháp giải hiệu quả trên, các em sẽ tự tin hơn khi giải các bài tập trong Mục 2 trang 76, 77, 78 SGK Toán 8 – Cánh diều. Chúc các em học tập tốt!