Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 8 tập 1 - Cánh diều, đặc biệt là mục 2 trang 31, 32, 33, 34.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
a) Tính số thích hợp vào
Video hướng dẫn giải
Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: \(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\)
Phương pháp giải:
Vận dụng các tính chất cơ bản của phân thức đại số để giải thích
Lời giải chi tiết:
\(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{\left( {3{\rm{x}} + y} \right).y}}{{y.y}} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\) (y là đa thức khác đa thức 0)
Video hướng dẫn giải
Cho phân thức: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}}\)
a) Tìm nhân tử chung của tử và mẫu
b) Tìm phân thức nhận được sau khi chia cả tử và mẫu cho nhân tử chung đó.
Phương pháp giải:
Dùng phương pháp phân tích các đơn thức thành tích của các thừa số để tìm nhân tử chung.
Lời giải chi tiết:
a) Ta có: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{2{\rm{x}}.2{\rm{x}}y}}{{3y.2{\rm{x}}y}}\)
Nhân tử chung của cả tử và mẫu là: 2xy
b) Chia cả tử và mẫu của phân thức đã cho cho nhân tử chung 2xy ta được:
\(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{\left( {4{{\rm{x}}^2}y} \right):2{\rm{x}}y}}{{\left( {6{\rm{x}}{y^2}} \right):2{\rm{x}}y}} = \dfrac{{2{\rm{x}}}}{{3y}}\)
Video hướng dẫn giải
Rút gọn mỗi phân thức sau:
\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}}\) \(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}}\)
Phương pháp giải:
Bước 1: Phân tử và mẫu thành nhân tử (nếu cần)
Bước 2: Tìm nhân tử chung của cả tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.
Lời giải chi tiết:
\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}} = \dfrac{{4{\rm{x}}.\left( {2{\rm{x}} + 1} \right)}}{{\left( {1 - 2{\rm{x}}} \right).\left( {1 + 2{\rm{x}}} \right)}} = \dfrac{{4{\rm{x}}}}{{1 - 2{\rm{x}}}}\)
\(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}} = \dfrac{{x\left( {{x^2} - {y^2}} \right)}}{{2{\rm{x}}\left( {x + y} \right)}} = \dfrac{{x\left( {x + y} \right)\left( {x - y} \right)}}{{2{\rm{x}}\left( {x + y} \right)}} = \dfrac{{x - y}}{2}\)
Video hướng dẫn giải
Cho hai phân thức \(\dfrac{1}{{{x^2}y}}\) và \(\dfrac{1}{{x{y^2}}}\)
a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.
b) Nhân xét gì về mẫu của hai phân thức thu được.
Phương pháp giải:
Thực hiện theo tính chất cơ bản của phân thức.
Lời giải chi tiết:
a) Ta có:
\(\dfrac{1}{{{x^2}y}} = \dfrac{{1.y}}{{{x^2}y.y}} = \dfrac{y}{{{x^2}{y^2}}}\)
\(\dfrac{1}{{x{y^2}}} = \dfrac{{1.x}}{{x{y^2}.x}} = \dfrac{x}{{{x^2}{y^2}}}\)
b) Mẫu của hai phân thức thu được giống nhau đều là: \({x^2}{y^2}\)
Video hướng dẫn giải
Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:
a) \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\)
b) \(\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}}\) và \(\dfrac{2}{{{x^2} - 25}}\)
Phương pháp giải:
Bước 1: Phân tích mẫu của mỗi phân thức rồi tìm MTC.
Bước 2: Tìm nhân tử phụ của mỗi phân thức (Bằng cách chia MTC cho từng mẫu)
Bước 3: Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng.
Lời giải chi tiết:
a) MTC chọn là: \(2{{\rm{x}}^2}{y^4}\)
Nhân tử phụ của \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\) lầm lượt là: y; 2x
Vậy: \(\begin{array}{l}\dfrac{5}{{2{{\rm{x}}^2}{y^3}}} = \dfrac{{5.y}}{{2{{\rm{x}}^2}{y^3}.y}} = \dfrac{{5y}}{{2{{\rm{x}}^2}{y^4}}}\\\dfrac{3}{{x{y^4}}} = \dfrac{{3.2{\rm{x}}}}{{x{y^4}.2{\rm{x}}}} = \dfrac{{6{\rm{x}}}}{{2{{\rm{x}}^2}{y^4}}}\end{array}\)
b) Ta có:
\(\begin{array}{l}\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}} = \dfrac{3}{{2{\rm{x}}\left( {x - 5} \right)}}\\\dfrac{2}{{{x^2} - 25}} = \dfrac{2}{{\left( {x - 5} \right)\left( {x + 5} \right)}}\end{array}\)
Chọn MTC là: \(2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)\)
Nhân tử phụ của các mẫu thức trên lần lượt là: \(\left( {x + 5} \right);2{\rm{x}}\)
Vậy:
\(\begin{array}{l}\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}} = \dfrac{3}{{2{\rm{x}}\left( {x - 5} \right)}} = \dfrac{{3\left( {x + 5} \right)}}{{2{\rm{x}}.\left( {x - 5} \right)\left( {x + 5} \right)}}\\\dfrac{2}{{{x^2} - 25}} = \dfrac{2}{{\left( {x - 5} \right)\left( {x + 5} \right)}} = \dfrac{{2.2{\rm{x}}}}{{2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)}} = \dfrac{{4{\rm{x}}}}{{2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)}}\end{array}\)
Video hướng dẫn giải
a) Tính số thích hợp vào ?: 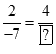 ;
; 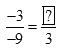
b) Hãy nhắc lại tính chất cơ bản của phân số.
Phương pháp giải:
Vận dụng quy tắc để hai phân số bằng nhau.
Lời giải chi tiết:
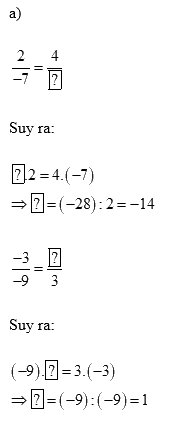
b) Tính chất cơ bản của phân số như sau:
- Nếu nhân cả tử và mẫu của một phân số với cùng một số tự nhiên khác 0 thì được một phân số mới bằng phân số đã cho:
\(\dfrac{a}{b} = \dfrac{{a.c}}{{b.c}}\left( {c \ne 0} \right)\)
- Nếu chia cả tử và mẫu của một phân số cho cùng một số tự nhiên khác 0 thì ta cũng được phân số mới bằng phân số đã cho.
\(\dfrac{a}{b} = \dfrac{{a:d}}{{b:d}}\left( {d \ne 0} \right)\)
Video hướng dẫn giải
a) Tính số thích hợp vào ?: 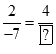 ;
; 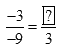
b) Hãy nhắc lại tính chất cơ bản của phân số.
Phương pháp giải:
Vận dụng quy tắc để hai phân số bằng nhau.
Lời giải chi tiết:
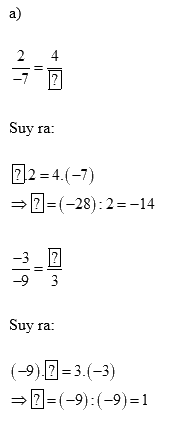
b) Tính chất cơ bản của phân số như sau:
- Nếu nhân cả tử và mẫu của một phân số với cùng một số tự nhiên khác 0 thì được một phân số mới bằng phân số đã cho:
\(\dfrac{a}{b} = \dfrac{{a.c}}{{b.c}}\left( {c \ne 0} \right)\)
- Nếu chia cả tử và mẫu của một phân số cho cùng một số tự nhiên khác 0 thì ta cũng được phân số mới bằng phân số đã cho.
\(\dfrac{a}{b} = \dfrac{{a:d}}{{b:d}}\left( {d \ne 0} \right)\)
Video hướng dẫn giải
Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: \(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\)
Phương pháp giải:
Vận dụng các tính chất cơ bản của phân thức đại số để giải thích
Lời giải chi tiết:
\(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{\left( {3{\rm{x}} + y} \right).y}}{{y.y}} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\) (y là đa thức khác đa thức 0)
Video hướng dẫn giải
Cho phân thức: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}}\)
a) Tìm nhân tử chung của tử và mẫu
b) Tìm phân thức nhận được sau khi chia cả tử và mẫu cho nhân tử chung đó.
Phương pháp giải:
Dùng phương pháp phân tích các đơn thức thành tích của các thừa số để tìm nhân tử chung.
Lời giải chi tiết:
a) Ta có: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{2{\rm{x}}.2{\rm{x}}y}}{{3y.2{\rm{x}}y}}\)
Nhân tử chung của cả tử và mẫu là: 2xy
b) Chia cả tử và mẫu của phân thức đã cho cho nhân tử chung 2xy ta được:
\(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{\left( {4{{\rm{x}}^2}y} \right):2{\rm{x}}y}}{{\left( {6{\rm{x}}{y^2}} \right):2{\rm{x}}y}} = \dfrac{{2{\rm{x}}}}{{3y}}\)
Video hướng dẫn giải
Rút gọn mỗi phân thức sau:
\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}}\) \(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}}\)
Phương pháp giải:
Bước 1: Phân tử và mẫu thành nhân tử (nếu cần)
Bước 2: Tìm nhân tử chung của cả tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.
Lời giải chi tiết:
\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}} = \dfrac{{4{\rm{x}}.\left( {2{\rm{x}} + 1} \right)}}{{\left( {1 - 2{\rm{x}}} \right).\left( {1 + 2{\rm{x}}} \right)}} = \dfrac{{4{\rm{x}}}}{{1 - 2{\rm{x}}}}\)
\(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}} = \dfrac{{x\left( {{x^2} - {y^2}} \right)}}{{2{\rm{x}}\left( {x + y} \right)}} = \dfrac{{x\left( {x + y} \right)\left( {x - y} \right)}}{{2{\rm{x}}\left( {x + y} \right)}} = \dfrac{{x - y}}{2}\)
Video hướng dẫn giải
Cho hai phân thức \(\dfrac{1}{{{x^2}y}}\) và \(\dfrac{1}{{x{y^2}}}\)
a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.
b) Nhân xét gì về mẫu của hai phân thức thu được.
Phương pháp giải:
Thực hiện theo tính chất cơ bản của phân thức.
Lời giải chi tiết:
a) Ta có:
\(\dfrac{1}{{{x^2}y}} = \dfrac{{1.y}}{{{x^2}y.y}} = \dfrac{y}{{{x^2}{y^2}}}\)
\(\dfrac{1}{{x{y^2}}} = \dfrac{{1.x}}{{x{y^2}.x}} = \dfrac{x}{{{x^2}{y^2}}}\)
b) Mẫu của hai phân thức thu được giống nhau đều là: \({x^2}{y^2}\)
Video hướng dẫn giải
Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:
a) \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\)
b) \(\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}}\) và \(\dfrac{2}{{{x^2} - 25}}\)
Phương pháp giải:
Bước 1: Phân tích mẫu của mỗi phân thức rồi tìm MTC.
Bước 2: Tìm nhân tử phụ của mỗi phân thức (Bằng cách chia MTC cho từng mẫu)
Bước 3: Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng.
Lời giải chi tiết:
a) MTC chọn là: \(2{{\rm{x}}^2}{y^4}\)
Nhân tử phụ của \(\dfrac{5}{{2{{\rm{x}}^2}{y^3}}}\) và \(\dfrac{3}{{x{y^4}}}\) lầm lượt là: y; 2x
Vậy: \(\begin{array}{l}\dfrac{5}{{2{{\rm{x}}^2}{y^3}}} = \dfrac{{5.y}}{{2{{\rm{x}}^2}{y^3}.y}} = \dfrac{{5y}}{{2{{\rm{x}}^2}{y^4}}}\\\dfrac{3}{{x{y^4}}} = \dfrac{{3.2{\rm{x}}}}{{x{y^4}.2{\rm{x}}}} = \dfrac{{6{\rm{x}}}}{{2{{\rm{x}}^2}{y^4}}}\end{array}\)
b) Ta có:
\(\begin{array}{l}\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}} = \dfrac{3}{{2{\rm{x}}\left( {x - 5} \right)}}\\\dfrac{2}{{{x^2} - 25}} = \dfrac{2}{{\left( {x - 5} \right)\left( {x + 5} \right)}}\end{array}\)
Chọn MTC là: \(2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)\)
Nhân tử phụ của các mẫu thức trên lần lượt là: \(\left( {x + 5} \right);2{\rm{x}}\)
Vậy:
\(\begin{array}{l}\dfrac{3}{{2{{\rm{x}}^2} - 10{\rm{x}}}} = \dfrac{3}{{2{\rm{x}}\left( {x - 5} \right)}} = \dfrac{{3\left( {x + 5} \right)}}{{2{\rm{x}}.\left( {x - 5} \right)\left( {x + 5} \right)}}\\\dfrac{2}{{{x^2} - 25}} = \dfrac{2}{{\left( {x - 5} \right)\left( {x + 5} \right)}} = \dfrac{{2.2{\rm{x}}}}{{2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)}} = \dfrac{{4{\rm{x}}}}{{2{\rm{x}}\left( {x - 5} \right)\left( {x + 5} \right)}}\end{array}\)
Mục 2 trong SGK Toán 8 tập 1 - Cánh diều thường tập trung vào các kiến thức về đa thức, các phép toán trên đa thức, và các ứng dụng của đa thức trong giải toán. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Bài 1: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 2: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 3: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 4: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 5: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 6: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 7: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Bài 8: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và ví dụ minh họa).
Trong quá trình giải bài tập, các em cần chú ý đến các quy tắc về dấu ngoặc, các quy tắc về phân phối, và các quy tắc về thứ tự thực hiện các phép toán. Ngoài ra, các em cũng nên rèn luyện kỹ năng kiểm tra lại lời giải để đảm bảo tính đúng đắn.
Hy vọng với lời giải chi tiết và dễ hiểu cho các bài tập mục 2 trang 31, 32, 33, 34 SGK Toán 8 tập 1 - Cánh diều, các em học sinh sẽ nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán. Chúc các em học tập tốt!